Traffic Jam
Emily's journey home took 25% longer than usual. By what percentage was her average speed reduced?
Age
14 to 16
Challenge level
Problem
Yesterday evening, Emily's journey home took $25\%$ longer than usual, as she was stuck in a traffic jam.
By what percentage was her average speed reduced compared to normal?
If you liked this problem, here is an NRICH task that challenges you to use similar mathematical ideas.
Student Solutions
Answer: 20%
Using inverse operations
100% + 25% = 1 + $\frac14$ = $\frac54$
time $\times$ speed = distance
Image
Image
Image
(new time) $\times$ (new speed) = distance
$\frac 54 \times$ ? = 1, so ? = $\frac45$ = 80%
80% of original time is a 20% reduction
Using a speed-time graph
Image
The area on a speed-time graph represents distance.
Green rectangle - normal day
Yellow rectangle - traffic jam
Image
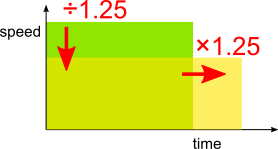
Horizontal scale factor $\times$ 125% = 1.25
So vertical scale factor is the inverse
$\div$ 1.25 = $\div \frac54$ = $\times \frac45$ = $\times$ 80%
80% of original time is a 20% reduction
Using algebra
Write $d$ for the distance of Emily's journey, and $t$ for the time it usually takes her. Then, in normal circumstances, her average speed is $\frac{d}{t}$.
Yesterday, her journey took $25\%$ longer than usual, meaning an increase of $0.25t$, so the time was $1.25t$. The distance was the same as usual.
Her average speed was therefore $\frac{d}{1.25t} = \frac{1}{1.25} \times \frac{d}{t} = 0.8\frac{d}{t}$. This means she travelled at $0.8$ of her usual average speed, which is a reduction of $0.2$ or $20\%$.