Tent Poles
Weekly Problem 40 - 2015
In the diagram, $PT = QT = TS$ and $QS = SR$. What is the value of $x$?
In the diagram, $PT = QT = TS$ and $QS = SR$. What is the value of $x$?
Age
11 to 14
Challenge level
Problem
Image
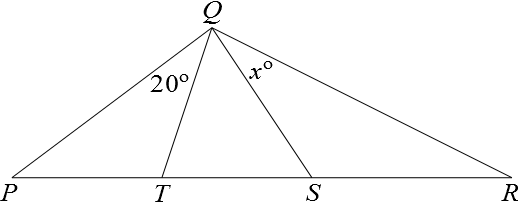
In the diagram,
$PT=QT=TS$
$QS=SR$
$\angle PQT=20^{\circ}$
What is the value of $x$?
If you liked this problem, here is an NRICH task that challenges you to use similar mathematical ideas.
Student Solutions
As $QS=SR$, triangle $SQR$ is isosceles, so $\angle SRQ= \angle SQR =x^{\circ}$.
So by the exterior angle theorem $\angle QST=2x^{\circ}$.
Also, $\angle TQS = 2x^{\circ}$ since $QT=TS$.
As $PT=QT$, $\angle TPQ=\angle TQP =20^{\circ}$.
Image
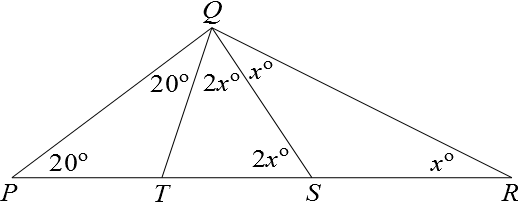
Since the interior angles of triangle $PQR$ must sum to $180^{\circ}$ we obtain $$20+(20+2x+x)+x=180$$ $$40+4x=180$$ $$4x=140$$ $$x=35.$$