Stolen pension
How much money did the pensioner have before being robbed?
Problem
A thief stole $\frac6{11}$ of a pensioner's money and spent $\frac6{11}$ of the money stolen. The thief was then caught, and the remaining money was returned to the pensioner.
The remaining money was £425 less than the amount the pensioner had after being robbed. How many pounds did the pensioner have before the theft?
This problem is adapted from the World Mathematics Championships
Student Solutions
Answer: £2057
Algebra
Started with $A$
$\frac6{11}A$ stolen, $\frac{5}{11}A$ left
$\swarrow$ $\searrow$
$\frac6{11}$ of $\frac6{11}A$ spent, $\frac5{11}$ of $\frac6{11}A$ recovered
Difference between money left and money recovered is $ £425$ $$\begin{align}
\tfrac5{11}A-\tfrac5{11}\times \tfrac6{11}A&=425\\
\Rightarrow \tfrac5{11}\left(1-\tfrac6{11}\right)A&=425\\
\Rightarrow \tfrac5{11}\times\tfrac5{11}\times A&=425\\
\Rightarrow A &= \tfrac{425}{25}\times121\\
\Rightarrow A&=2057
\end{align}$$
Using a diagram to represent the story
This diagram represents the story.
Image
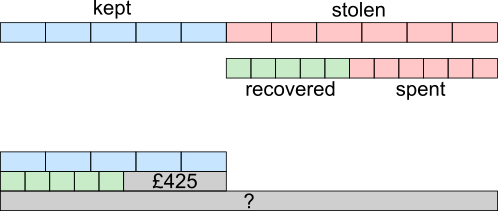
To compare the recovered and kept money, it would be useful if the pieces were the same size.
The 'stolen' money is split into 6 parts by the pensioner, but into 11 parts by the thief. This means that we can split it into 66 pieces.
Image

55$-$30 = 25, so £425 is equivalent to 25 pieces.
If 25 pieces are worth £425, then each piece is worth £425$\div$25 = £17.
So 121 pieces are worth 121$\times$ £17 = £2057.
