Space distances
Problem
In the picture below you can see the orbits of Mercury, Venus, Earth (this label is slightly hidden) and Mars, along with the orbit of an asteroid called Florence (named after Florence Nightingale).
The picture shows their positions in August 2017. Florence was at its nearest position to Earth at the start of September 2017.
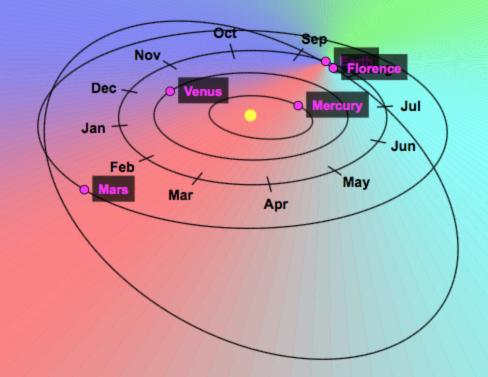
Florence's distance from the Sun varies from 150 000 000km at its nearest (during summer 2017) to 375 000 000km when furthest away.
Starting when Florence is nearest to the sun, what distance will it be from the Sun after travelling...
1) 100 km further from the Sun?
2) 1 000 km further from the Sun?
3) 10 000 km further from the Sun?
4) 100 000 km further from the Sun?
5) 1 000 000 km further from the Sun?
Starting with Florence furthest from the sun, what distance will it be from the Sun after travelling...
6) 100 km nearer the Sun?
7) 1 000 km nearer the Sun?
8) 10 000 km nearer the Sun?
9) 100 000 km nearer the Sun?
10) 1 000 000 km nearer the Sun?
Student Solutions
Well done to everybody who calculated these space distances. Lots of children sent in the answers, but only a few children explained their working.
The children from Wallbrook Primary in the UK said:
To answer the questions 1-5, you needed to find the starting figure which was 150,000,000km. We then had to add individual powers of ten for each question e.g. 150,000,000km + 1,000km = 150,001,000km.
To answer questions 6-10, we started with 375,000,000km and then subtracted each individual power of ten e.g. 375,000,000km - 100,000km = 374,900,000km. Another example is 375,000,000km - 100km = 374,999,900km. An easy mistake to make would be to think 9s would appear in every column. To check we were correct, we had to add our power of ten to our answer to make sure it added up to our starting number.
Esther and Zaki from the Bristol Hospital Education Service in the UK noticed some patterns in their answers. Zaki said:
When I started the addition problems, I noticed that the number I was adding got 10x bigger each time. In the sum, the '1' moved up the place value columns by one column each time. After the first couple of calculations, I was able to use the pattern to predict the calculations.
Although I added each distance separately, I could also easily calculate how much the total would be if I combined all of the extra distances in one sum.
I predicted there would be a similar pattern in the subtraction because the number being subtracted also got 10x bigger each time. I found that in the answer, the '9's disappeared from the place value columns one by one as the amount being subtracted got larger.
Esther sent in this picture and talked about the patterns in the numbers:
Thank you all for sharing your ideas with us!
Teachers' Resources
Space Distances
In the picture below you can see the orbits of Mercury, Venus, Earth (this label is slightly hidden) and Mars, along with the orbit of an asteroid called Florence (named after Florence Nightingale).
The picture shows their positions in August 2017. Florence was at its nearest position to Earth at the start of September 2017.
Florence's distance from the Sun varies from 150 000 000km at its nearest (during summer 2017) to 375 000 000km when furthest away.
Starting when Florence is nearest to the sun, what distance will it be from the Sun after travelling...
1) 100 km further from the Sun?
2) 1 000 km further from the Sun?
3) 10 000 km further from the Sun?
4) 100 000 km further from the Sun?
5) 1 000 000 km further from the Sun?
Starting with Florence furthest from the sun, what distance will it be from the Sun after travelling...
6) 100 km nearer the Sun?
7) 1 000 km nearer the Sun?
8) 10 000 km nearer the Sun?
9) 100 000 km nearer the Sun?
10) 1 000 000 km nearer the Sun?
Why do this problem?
This activity offers an opportunity to count forwards and/or backwards in steps of powers of ten.
Possible approach
Present the picture and ask the group to 'say what they see'. This allows all children to take part and sets the scene for the task. You will need to provide them with some of the information given in the text and then you can faciliate a discussion about Florence's journey.
You may wish to tackle the questions as a whole group, perhaps giving children time to think individually before talking to a partner, then sharing with everyone.
Key questions
How are you working out your answers?
Could you think of some other questions to ask about this?
Possible extension
Ask the pupils to think up their own challenges to give one another but they need to know the correct answers themselves!