So big
One side of a triangle is divided into segments of length a and b
by the inscribed circle, with radius r. Prove that the area is:
abr(a+b)/ab-r^2
Problem
Image
|
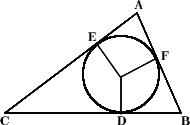
A circle of radius $r$ is drawn inside a triangle so that it
just touches each of the three sides as shown in the diagram. The
three corners and points where the circle touches have been
labelled $A$ to $F$.
One side of the triangle is divided into segments of length
$a$ and $b$ by the inscribed circle. However, we are not told which
of the three sides is divided in this way.
From this information we can find an expression for the area
of the triangle. Prove that the area of the triangle is:
$$\frac{abr(a+b)}{ab-r^2}. $$
|
Getting Started
What can you say about the tangents of the angles at the centre of the circle?
Alternatively, can you see how you might calculate the area of these 6 smaller triangles?
Image
Student Solutions
Eduardo from the British School, Manila, Tomas from Malmesbury School and Philip used the tangent formula and Alex and also Sue Liu of Madras College, St Andrew's sent a solution to this problem which depends on the use of Heron's Formula for the area of a triangle. Well done all of you.
Image
|
FIRST
METHOD
Using the tangents of the angles at the centre of the circle
and the formula
$\tan X= -\tan(A + B) =\frac{\tan A + \tan B} {\tan A \tan B -
1} $ where $A + B + X = 180^o$,
$\frac{x}{r}= \frac{\frac{a}{r} + \frac{b}{r}}{\frac{ab}{r^2}-1} = \frac{r(a + b)}{ab - r^2}.$The area of the triangle is $(a + b + x)r = (a + b)r +
\frac{r^3(a + b)}{ab - r^2}= \frac{(a + b)abr}{ab - r^2}$ as
required.
|
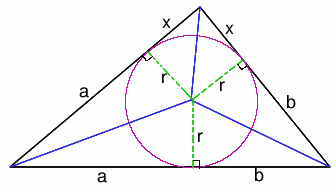
SECOND METHOD
This method uses Heron's formula. The lines from the centre of the circle to the edges each meet the tangents to the circle forming right angles as shown. The triangle has been rotated/reflected so that the side with length (a+b) is the base. (However it is rotated it is the same shape of unknown angles and lengths). As the tangents to a circle from an external point are equal in length (easily proved using congruent triangles) the other lengths of the sides of the triangle can be found. The incircle divides the sides of the triangle into lengths $c' = a + b$, $b' = b + x$ and $a' = x + a$ as shown in the diagram.
The semi-perimeter of the triangle is given by $s = x + a + b$ and from Heron's formula the area of the triangle is
$A = \sqrt{(s(s - a')(s - b')(s -
c'))}$
$= \sqrt{((a + b + x)abx)} $
Also, the triangle is divided into three smaller triangles and the total area is given by
$ A = \frac{1}{2}(a + b)r +
\frac{1}{2}(b + x)r + \frac{1}{2}(x + a)r $
$=(a + b + x)r $.
Equating the two answers
$ \sqrt{abx(a + b + x)} = (a + b +
x)r $
$ abx(a + b + x) = (a + b + x)^2
r^2 $
$ abx = (a + b + x)r^2 $
$x = \frac{(a + b)r^2}{ (ab -
r^2).} $
Hence
$ A = (a + b + x)r$
$ = \frac{r((a + b)(ab - r^2) + (a
+ b)r^2)}{ ab - r^2}$
$ = \frac{abr(a + b)}{ab - r^2.}
$
An alternative method, not using Heron's formula, is based on finding $x$ in terms of $a$ and $b$ using the tangents of the angles at the centre of the circle.
Teachers' Resources
Why do this problem?
At first sight there might not seem to be enough information given in this question to find a solution. The first step is to interpret what is known from the geometry given the inscribed circle, and then to evaluate that information in terms of how it might be used to express what is known in terms of the three variables $a$, $b$ and $r$ and how that might be used to give an expression for the area of the triangle.One of the methods of solving this problem is an application of the formula for tan$(A + B)$ combined with the formula for the area of a triangle.
Possible approach
Set this as an exercise in applying the formula for $tan(A + B)$ or better still, if you want the students to revise their trigonometry, you can make it a more challenging problem solving activity and leave it to the students to decide what they have to use.Key questions
Can we make a list of everything that is known from the information given?Can we see a way of using the information given to find the area of the triangle?
Can we add lines to make pairs of congruent triangles?
Can we find the area of the whole triangle in terms of these smaller congruent triangles?
What can we say about the angles at the centre of the circle?
If three of the angles at the centre add up to $180$ degrees what can we say about the tangents of these angles?
