Seven squares
Watch these videos to see how Phoebe, Alice and Luke chose to draw 7 squares. How would they draw 100?
Problem
Seven Squares printable sheet - seven squares pattern
Seven Squares printable sheet - more patterns
Three students were asked to draw this matchstick pattern:

This is how Phoebe drew it:
Can you describe what Phoebe did?
How many 'downs' and how many inverted C's are there?
How many matchsticks altogether?
Now picture what Phoebe would do if there had been $25$ squares.
How many 'downs' and how many inverted C's would there be?
How many matchsticks altogether?
If there had been $100$ squares? How many matchsticks altogether?
A million and one squares? How many matchsticks?
This is how Alice drew it:
Can you describe what Alice did?
How many 'alongs' and how many 'downs' are there?
How many matchsticks altogether?
Now picture what Alice would do if there had been $25$ squares.
How many 'alongs' and how many 'downs' would there be?
How many matchsticks altogether?
If there had been $100$ squares? How many matchsticks altogether?
A million and one squares? How many matchsticks?
This is how Luke drew it:
Can you describe what Luke did?
How many squares and how many inverted C's are there?
How many matchsticks altogether?
Now picture what Luke would do if there had been $25$ squares.
How many squares and how many inverted C's would there be?
How many matchsticks altogether?
If there had been $100$ squares? How many matchsticks altogether?
A million and one squares? How many matchsticks?
Now choose a couple of the patterns below.
Try to picture how to make the next, and the next, and the next...
Use this to help you find the number of squares, or lines, or perimeter, or dots needed for the $25^{th}$, $100^{th}$ and $n^{th}$ pattern.
Can you describe your reasoning?
Growing rectangles
This rectangle has height 2 and width 3.

- height 2 and width 25
- height 2 and width 100
- height 2 and width n
L Shapes

- height 25 and width 25
- height 100 and width 100
- height n and width n
Two squares

- 25 black dots
- 100 black dots
- n black dots
Square of Squares

- side length 25
- side length 100
- side length n
Dots and More Dots
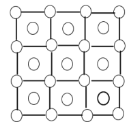
- side length 25
- side length 100
- side length n
Rectangle of Dots

- side length 25
- side length 100
- side length n
Getting Started
How did Phoebe group the matchsticks that she drew?
How did Alice and Luke group their matchsticks?
For the follow-up activities, draw them out for yourself and notice how YOUR drawings develop.
Always begin with simple cases and try to PREDICT what will happen.
Look for patterns.
How can you describe the lines? Horizontal? Vertical?
Try to understand why the patterns develop in the ways that they do.
Student Solutions
Alexander, from Wilson's School, wrote:
Phoebe first drew one "down," and then as many "inverted Cs" as needed to get seven squares. Therefore:
- When drawing only seven squares you draw one "down" and seven "inverted Cs." There were 22 matchsticks.
- When drawing 25 squares, there would still be one "down," but 25 "inverted Cs." The total number of matchsticks would be 76.
- When drawing 100 squares, again there would be only one "down," but 100 "inverted Cs." The total number of matchsticks would be 301.
- When drawing 1,000,001 squares, there would be 1 "down" and 1,000,001 "inverted Cs." There would be 3,000,004 matchsticks.
- When drawing n squares, there would be one "down" and n "inverted Cs." There would be 3n + 1 matchstick(s). This is because there is one matchstick at the beginning that forms the "down," and then each of the "inverted Cs" takes up three matchsticks, so you multiply the number of inverted Cs by three and then add 1.
Alice first drew seven "alongs" at the top, and then seven "alongs" at the bottom. She then used eight "downs" to connect the gaps in between two parallel "alongs." Therefore:
- For seven squares you draw fourteen "alongs" and eight "downs." The total number of matchsticks is 22.
- When drawing 25 squares, you draw 50 "alongs" and 26 "downs," making the total number of matchsticks 76.
- When drawing 100 squares, you draw 200 "alongs" and 101 "downs," making the total number of matchsticks 301.
- When drawing 1,000,001 squares, you draw 2,000,002 "alongs" and 1,000,002 "downs," making the total 3,000,004 matchsticks.
- When drawing n squares, you draw 2n "alongs" and n + 1 "downs," making the total 3n + 1 matchsticks. This works because for each square, there are two "alongs," and like an "inverted C," you have one "down" for each square, but then you add one more "down," because like Phoebe's method, you need one extra line at the end. Adding the two formulas together, 2n + n + 1 = 3n + 1, which is the same as Phoebe's formula.
Luke first drew one "square," and then six "inverted Cs" to make seven squares. Therefore:
- You need one "square" and six "inverted Cs" to make seven squares. This gives you a total of 22 matchsticks.
- Similarly, with 25 squares, you draw one "square," but 24 "inverted Cs," which gives you a total of 76 matchsticks.
- With 100 squares, you still draw one "square," but 99 "inverted Cs," which gives you a total of 301 matchsticks.
- With 1,000,001 matchsticks, again you draw one "square," but you draw 1,000,000 "inverted Cs," giving you a total of 3,000,004 matchsticks.
- With n matchsticks, you draw one "square," and n - 1 "inverted Cs," giving you a total of 3n + 1 matchsticks:
4 + 3(n - 1) = 4 + 3n - 3 = 3n + 1,
which is the same as all of the other methods.
Great! Laeticia, from Woodbridge High School, also gave correct general formulas here. She went on to comment on one of our later puzzles:
Growing rectangles:
If the height is h and the width is w, then the perimeter is 2h + 2w. Then there are (h+1)(w+1) dots, and w(h+1) + h(w+1) lines.
Niharika solved the rest of our questions:
L-shapes:
Each L-shape has an 'inner' L-shaped line and an 'outer' L-shaped line. If an L-shape has height and width n, then the outer L has length 2n and the inner L has length 2(n-1). There are 2 lines remaining on the ends of the L, so altogether the perimeter is 4n.
There are 2(n-1) lines left inside the L-shape, so the shape is made of 6n - 2 lines.
The number of squares in an L-shape is 2n-1: think of each L as two rectangles of height 1 and width n that overlap in one square.
Two squares:
Think of these as two separate overlapping squares, each with $n^2$ dots. They overlap in one dot, so in total there are $2n^2 - 1$ dots, and so $2n^2 - n - 1$ white dots.
In each square there are 2n(n-1) lines, and the lines never overlap, so in total there are 4n(n-1) lines.
Square of squares:
We can split a pattern like this of side length n up into four rectangles of height 1 and length n-1, so there are 4(n-1) edge squares.
There are 4n lines making up the outer square and 4(n-2) lines making up the inner square. There are 4(n-1) lines left in the middle. This gives 12(n-1) lines in total.
Dots and more dots:
Inside the squares there are $n^2$ dots, and on the vertices there are $(n+1)^2$ dots, so in total there are $2n^2 + 2n + 1$ dots.
In each row there are n lines, and there are n+1 rows, so the rows contribute n(n+1) lines. Similarly the columns contribute n(n+1) lines, so together there are 2n(n+1) lines.
Rectangle of dots:
There are 4n horizontal lines and 3n vertical lines, so 7n lines in total.
On each row there are 2n+1 dots, and there are n+1 rows, so there are (2n+1)(n+1) dots.
Fantastic! Thank you all.
Teachers' Resources
Why do this problem?
This problem challenges students to describe patterns clearly - verbally, numerically and algebraically. It does not assume prior knowledge of algebra and could be a good way to introduce, practise or assess algebraic fluency.
Similar-looking questions are often asked, expecting an approach that uses number sequences for finding a formulae for the $n^{th}$ term. This problem deliberately bypasses all that, instead focusing on the structure of the pattern so that the algebraic expressions emerge naturally from that structure.
Possible approach
Have the "seven squares" image preprepared on the board so that students cannot see how you drew it. "I have drawn seven matchstick squares on the board, and I would like you to make a rough copy of it - no need to use a ruler."
While the students are sketching, look out for students creating the image in different ways, such as Phoebe's, Alice's and Luke's methods in the problem.
Select at least three students who have used different methods, and invite them to draw the image on the board (perhaps using colours to emphasise the order in which it was drawn).
"Without counting individual matches can you say how many matchsticks there are in the drawing?"
Alternatively, you could show the class the videos provided in the problem showing three different methods.
Next, hand out this worksheet. There are six different patterns with the simpler ones at the start. Invite students to work in pairs:
"With your partner, choose two or three of the six patterns and have a go at the questions. Make sure you can explain clearly how you worked out your answers, focusing on the order in which you would draw the diagram, like we did for the Seven Squares problem."
While students are working, circulate and listen to the conversations, identifying students who have really elegant ways of seeing the general case in the initial picture.
"I'm going to give you ten minutes to prepare a poster presenting one of the problems you worked on and explaining how you arrived at your solution."
Students could choose which problem to work on, and you could guide particular students towards problems where you have noticed them reasoning clearly.
Once they have produced their poster, there are a number of different ways that sharing and feedback could be organised:
- Half the class stand by their posters and the other half of the class visit them, read, ask for clarification on anything that is unclear, and suggest improvements as 'critical friends'. After five minutes, swap over.
- All the posters are laid out. Students visit each other's posters and write any comments, questions or feedback on post-it notes.
- Selected students could present the content of their poster on the board, with the rest of the class feeding back.
Key questions
Possible support
Encourage students to draw a few examples of each pattern and notice how their drawings develop.
Possible extension
Here are a couple of suitable follow-up problems that use the structure of a situation to lead to algebraic generalisations:
