Same Answer
Aisha's division and subtraction calculations both gave the same answer! Can you find some more examples?
Problem
Aisha has been practising arithmetic with fractions.
She worked out $4\frac{1}{2} - 3$ but then she realised that she had misread the question, and the teacher had actually asked her to work out $4\frac{1}{2} \div 3$
When she worked out the division, she was surprised to find she got the same answer to both calculations!
Aisha decided to look for other calculations where replacing the division sign by a subtraction sign does not alter the result of the calculation.
Here are some of the examples she tried:
$3\frac12 - 2$ and $3\frac12 \div 2$
$5\frac12 - 4$ and $5\frac12 \div 4$
$5\frac13 - 4$ and $5\frac13 \div 4$
$6\frac17 - 5$ and $6\frac17 \div 5$
$7\frac15 - 6$ and $7\frac15 \div 6$
Which of Aisha's examples give the same answer for both calculations?
Can you spot any patterns?
Click below to see two different observations about the examples where the answer is the same.
"I noticed that in the examples that worked, the denominator in the fraction was one less than the number being subtracted."
"I drew a diagram to help me understand:"
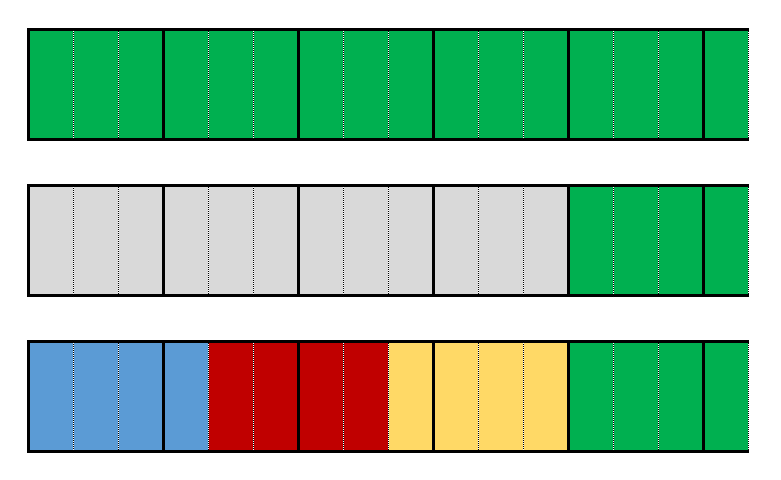
The top shows $5\frac13$.
The second row shows $5\frac13-4$
The third row shows $5\frac13\div4$."
Can you find a general rule?
Extension:
Can you justify this rule algebraically?
What happens if you replace the subtraction sign with an addition sign?
With thanks to Don Steward, whose ideas formed the basis of this problem.
Getting Started
$5\frac13 = 4+ 1\frac13 = 4+ \frac43$
What happens when you subtract 4?
What happens when you divide by 4?
If I want to divide a number by 5, and I want the answer to be the same as when I subtract 5, what can you say about my number?
It's going to be around 6...
Student Solutions
Navjot from Sherborne Qatar, Nond and Temin from Bangkok Patana School in Thailand, Kit and Fiennes from Sandroyd School in the UK, Agatha, Jasmine and Kayla from North London Collegiate School in the UK, Shriya from International School Frankfurt in Germany and Lucy from Northgate School in the UK told us which of Aisha's examples gave the same answer. This table is from Agatha, Jasmine and Kayla's work:
Kit, Arthur, Lily-Rose and Alex from Sandroyd School and Shriya also sent us their own examples.
Shriya, Kit, Alex and Lily-Rose found that $ 9 \frac 17 -8 = 1\frac17$ and $9\frac17\div8=\frac{64}7\div\frac81 = \frac{64}7\times 1 8 = \frac 87 = 1\frac17$
Alex and Shriya found $11 \frac 19 - 10$ and $11\frac 19\div10$
Shryia also found that:
$6\frac14 - 5 = 6\frac14\div5=1\frac14$
$8\frac16 - 7 =8\frac16\div7=1\frac16$
$10\frac18-9=10\frac18\div9=1\frac18$
Agatha, Jasmine and Kayla looked for patterns, and had some ideas which didn't work:
Agatha thought that "the rule was that when an odd denominator is subtracted by an odd number and vice versa, they would work." We tried this rule with other numbers, but we found it didn't always work. eg. $3\frac17-2$ and $3\frac17\div2$
"The pattern is when the denominator is a multiple of the number you are subtracting/dividing" said Kayla. Soon, we realised it was wrong.
Michelle from Dulwich College Seoul in South Korea found a pattern:
So, while I was solving the examples I found a pattern between the mixed number and the dividing number.
For example :
$7 \frac 15-6$ and $7 \frac 15\div6$
So when the mixed number ($7\frac15$) is converted into an improper fraction, the dividing number ($6$) is a factor of the numerator of the improper fraction.
$7 \frac 15 - 6$ $7 \frac 15 \div 6$
$= \frac{36}5 - \frac{30}5$ $= \frac{36}5 \times\frac 16$
$ = \frac65$ $=\frac 65$
As you can see $6$ (the dividing number) is a factor of $36$ (the numerator of the improper fraction).
Tilly from the UK and Nond and Temin were more specific. Nond and Temin said:
If you change the mixed fractions to improper fractions, the numerator is a square number and the square root of the numerator is the number that you are subtracting or dividing:
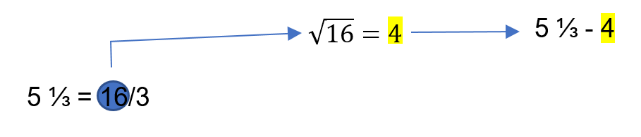
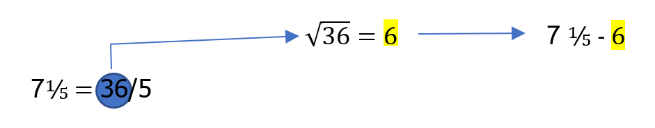
Tilly also noticed that:
The denominator of the mixed number is the integer of the mixed number subtract 2 (5 and 3 in the top example, 7 and 5 in the second)
The sum of the numerator and the denominator in the mixed number is equal to the number that is subtracted.
Nond and Temin said additionally that the numerator was always 1.
Nond and Temin, Fiennes, Lily-Rose and Shriya described a general rule. Fiennes said:
I saw that the whole number at the front was 2 more than the denominator and 1 more than the number after the minus or the division symbol.
Navjot and Lucy expressed this pattern algebraically, and then both proved that numbers which follow this pattern always give the same answer. Navjot said:
Generalising this, the division of a mixed fraction and a positive integer and the difference between the two will work when the expression is in the form $(n+2)\#\frac1n -(n+1)$, or $(n+2)\#\frac 1 n \div(n+1)$, either is fine since they will give the same answer anyway.
Navjot decided to use the $\#$ to represent a mixed number, since $(n+2)\frac1n$ usually means $(n+2)\times\frac1n$, but here it's a mixed number.
Lucy used $+$ instead, since $1\frac12$ means $1+\frac12$, not $1\times\frac12$. This is Lucy's proof:
This was the equation I created (by taking $x$ as the denominator of the fraction).
$$\left((x+2) +\frac1x \right) - (x+1) = \left((x+2)+ \frac1x\right) ÷ (x+1)$$
I then knew that I needed to simplify the fraction to create both the sides of the equation to equal the same thing as that would prove my equation would always work.
I started off by multiplying both sides of the equation by the $x+1$, which left me with the equation:
$$ \left(x^2 + 3x +2 + \frac{1+x}{x}\right) - \left(x^2+ 2x + 1\right) = (x+2) + \frac1x$$
Then I focused on the first side and simplified it by [expanding] the bracket away from that side, so it ended up like this:$$x + 1 + \frac{1+x}x = x+2 +\frac1x$$
I then took $x + 1$ off both sides to leave me with: $$\frac{1+x}x = 1 +\frac1x$$
I then had to simplify the second side, as the $1$ could be added to the fraction because $1$ is equal to $\dfrac xx$ (like this $\dfrac11 + \dfrac xx$): $$\dfrac{1+x}x = \dfrac{1+x}x$$
I ended up with what I had expected, which was both sides of the equation equalling the same answer, which in turn proves my theory as being correct.
Navjot tested whether this works when $n$ (or '$x$') is negative:
However, using this expression doesn't work with negative integers.
Example: Let $n = -5$
Subtraction:
$-3\#\frac1{-5} -(-4) =\frac{16}5 + 4 =\frac{36}5$
Division:
$-3\#\frac 1{-5} \div (-4) = \frac{16}5 \div -4 =16\div(-20) = -\frac45$
$\frac{36}5 ≠ -\frac45$
However, really, $-3\#\frac1{-5}$ has both the whole number and the fraction negative, so should be $-\frac{16}5$ (Navjot has used $+\frac{16}5$). So in this case the 'subtraction' would be $-\frac{16}5 + 4 = \frac 45$, and the division would be $-\frac{16}5\div(-4) = -\frac45$. So they still give the same result - but now the subtraction has become an addition.
Jack from Ashmole Academy and James from Sainsbury School, both in the UK, both found algebraic expressions for the numbers without building a conjecture first. This is James' work:
Posing the first number as $a$ and the second number as $b$, the problem becomes:
For which $a,b$ belonging to the real numbers does$$a-b=\frac ab$$
The problem looks different now - but here $a$ represents Aisha's mixed number, and $b$ is the number which can be either divided by or subtracted.
We get with simple algebra
$$\begin{align} ab-b^2&=a\\
\Rightarrow ab-a&=b^2\\
\Rightarrow a(b-1)&=b^2\\
\Rightarrow a&=\frac{b^2}{b-1}\end{align}$$
This gives us a formula to generate $a$'s with $b$'s as an input.
Therefore the answer couplets are:
$$\begin{align}&(a,b)=\left(\frac{b^2}{b-1},b\right)\\
\Rightarrow& (a,b)=\left(\frac{(b+1)(b-1)+1}{b-1},b\right)\\
\Rightarrow&(a,b)=\left((b+1)+\frac1{b-1},b\right)\end{align}$$
which explains her observation
If we go through the same algebra but instead replace the subtraction sign with an addition sign we get the answer couplets: $$(a,b)=\left(-\frac{b^2}{b-1},b\right)$$ Notice that this is equivalent to $$(a, b) = \left(-\left((b+1)+\frac1{b-1}\right),b\right)$$ which is the same as the result obtained from substituting negative numbers into Navjot's equation.
Jack began with something that looked more like Aisha's working, but having three unknowns rather than two made the algebra more complicated:
Primarily, let the improper fraction be written as $\frac ab$, where $a > b$, and both $a$ and $b$ are positive integers. Also, let $c$ be the value that we wish to subtract and divide from the fraction. Using this notation, we can form the equation: $$\frac ab-c = \frac ab\div c$$
Finding a common denominator in the LHS, and evaluating the RHS, we can simplify the above equation into: $$\frac ab - \frac{bc}b = \frac a{bc} \hspace{8mm} \Rightarrow\hspace{8mm} \frac{a - bc}b = \frac a{bc}$$
We can now cross multiply to get rid of the fractions: $$(a - bc)(bc) = ab \hspace{8mm}\Rightarrow \hspace{8mm}abc - (b^2)(c^2) = ab$$
Now, as all of the terms in the equation have a factor of $b$, we can divide both the RHS and LHS by $b,$ leaving us with a quadratic equation: $$ac - bc^2 = a \hspace{8mm}\Rightarrow \hspace{8mm}bc^2 - ac + a = 0$$
Just for simplicity, let $a = y$, $b = w$ and $c = x$, (so we do not get muddled up when we use the quadratic formula next):$$wx^2 - yx +y = 0$$
We can now use the quadratic formula to find $x$ in terms of $w$ and $y$ (the quadratic formula being $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$ ): $$x = \frac{y \pm \sqrt{y^2 - 4wy}}{2w}$$ or converting back to $a, b$ and $c$: $$c = \frac{a \pm \sqrt{a^2 - 4ab}}{2b}$$
HOWEVER, $c$ will ONLY be real iff (IF AND ONLY IF) $a^2 - 4ab \ge 0$ (as the square root of a negative number is impossible in the real plane).
Thus, we can solve the above above inequality:
$a^2 - 4ab \ge 0$ Factorise out $a$, so $a(a - 4b) \ge 0$
The expression $a(a - 4b)$ has roots at $a=0$, and at $a=4b$, thus, we find that either:
$a \le 0$, which is not accepted as a is a positive integer, or
$a \ge 4b$, which we can allow.
Thus, we have proven that for ANY 2 positive integers $a$ and $b$ (where $a\ge 4b$), there exists a value $c$* (which is $\dfrac {a \pm \sqrt{a^2 - 4ab}}{2b}$) such that $\frac ab - c = \frac ab \div c.$ Or in other words, if Aisha's mixed fraction is converted into an improper fraction, and the numerator is greater than or equal to 4 times the denominator, there is a number which when divided or subtracted from the fraction gives the same result either way. QED.
* The value of $c$ is not necessarily an integer: but for it to be rational, $a^2 - 4ab$ must be a square number, and for it to be an integer, $2b$ must be a factor of $a + \sqrt{a^2 - 4ab}$
Teachers' Resources
Why do this problem?
Even if they have met calculation with fractions before, students often need more practice. It is important to address this without it feeling like an exact repetition of what they have done many times before. This problem lets you spot misconceptions your students have about subtraction and division of fractions, while giving students an opportunity to practice the procedures in an intriguing context - students' curiosity will be raised by the strange patterns in the calculations, and we hope they will yearn to explain what is happening.
Possible approach
Share the following problem with the class:
Aisha has been practising arithmetic with fractions.
She worked out $4\frac{1}{2} - 3$ but then she realised that she had misread the question, and the teacher had actually asked her to work out $4\frac{1}{2} \div 3$
When she worked out the division, she was surprised to find she got the same answer to both calculations!
Firstly you might like to ask the class to verify the claim. Use this time to circulate and look for students who may need a reminder of how to calculate with fractions. You may also find students using different strategies and it would be worth sharing some of these with the class.
Once you have agreement and some strategies to use you could ask your students to try out some more examples.
Which of the following pairs of statements are equal?
$3\frac12 - 2$ and $3\frac12 \div 2$
$5\frac12 - 4$ and $5\frac12 \div 4$
$5\frac13 - 4$ and $5\frac13 \div 4$
$6\frac17 - 5$ and $6\frac17 \div 5$
$7\frac15 - 6$ and $7\frac15 \div 6$
Give students some time to calculate each example and check for themselves.
Once everyone has figured out which ones are equal, write them on the board in a list.
Students may make the following observations:
- The denominator of the fraction is 1 less than the number being subtracted.
- The whole number part is 1 more than the number being subtracted.
Invite students to try some more examples based on any observations they have made, and to see if they can explain why they work. While students are working, take a look at what they're doing and invite students working on any interesting representations to share them with the class.
You might like to share the representation from the problem as a prompt.

The top shows $5\frac13$.
The second row shows $5\frac13-4$
The third row shows $5\frac13\div4$.
Possible support
For a similar idea with adding and multiplying fractions students could work on Sum Equals Product.
Possible extension
Students who are comfortable using algebra could be asked to represent their results algebraically.
Fair Shares is another example of a fractions problem that leads to algebra and some generalisation.
