The roller and the triangle
How much of the inside of this triangular prism can Clare paint using a cylindrical roller?
Problem
Clare is painting the inside of a short triangular prism with a roller. The cross-section of the prism is an equilateral triangle with side length 1, and the cross-section of the roller is a circle with circumference 1. This is shown in the diagram.
Image
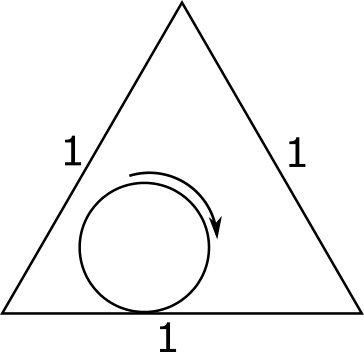
What is the total length that Clare can paint?
Give an exact answer.
This problem is adapted from the World Mathematics Championships
Student Solutions
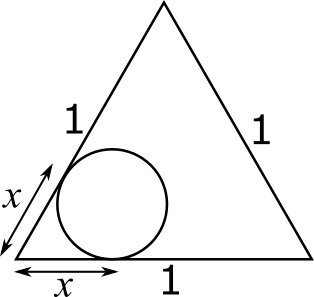
The circle won't fit into the corners of the triangle, so it won't touch some of the parts of the perimeter of the triangle. The parts that it won't touch are the parts that Clare can't paint with the roller, and they are labelled $x$ on the diagram below.
Image
Using the radius of the circle, two right-angled triangles can be made which contain $x$, as shown below (they are right-angled because the angle between the tangent and the radius is 90$^{\text{o}}$).
Image
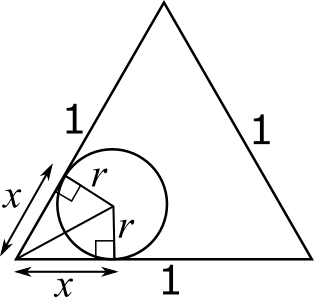
The radius of the circle can be found using the formula circumference = $\pi\times$2$r$, so $1=2\pi r$, so $r=\dfrac{1}{2\pi}$.
Using trigonometry
Since the two right-angled triangles drawn share all three sides, they are congruent, so the 60$^{\text{o}}$ angle of the triangle must be bisected to give two 30$^{\text{o}}$ angles.
This gives the triangle shown below.
Image
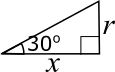
$\tan{30}=\dfrac{r}{x}$, and since $r=\dfrac{1}{2\pi}$ and $\tan{30}=\dfrac{1}{\sqrt{3}}$, $$\begin{align}\dfrac{1}{\sqrt{3}}&=\dfrac{\frac{1}{2\pi}}{x}\\
\dfrac{x}{\sqrt{3}}&=\dfrac{1}{2\pi}\\
x&=\dfrac{\sqrt{3}}{2\pi}\end{align}$$
So the circle will touch all of the perimeter of the triangle, which is 3, except for $x$ twice at each corner. So The circle will touch $3-6x=3-6\dfrac{\sqrt{3}}{2\pi}=3-\dfrac{3\sqrt{3}}{\pi}$.
Using similar triangles and Pythagoras' theorem
If the line from the corner of the triangle is extended, it will cut the triangle exaclty in half, since it goes through the centre of the circle and the circle and the triangle are both symmetrical. This is shown below.
Image
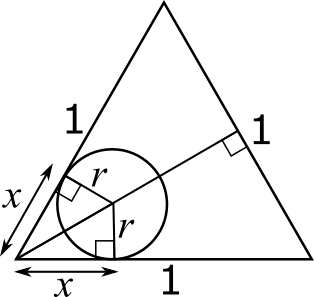
The larger right-angled triangle in the diagram is similar to the smaller right-angled triangles. This is shown again across the two diagrams below, where the dark red angles are equal (because the triangle is cut exactly in half), and corresponding sides are the same colours.
Image
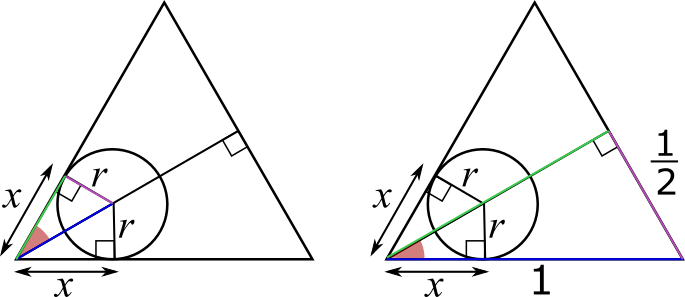
$x$ corresponds to the green side, so if we find the length of the green side on the larger triangle, and the scale factor between the triangles, then we can find $x$.
The triangles are shown again below with some of the extra information removed.
Image
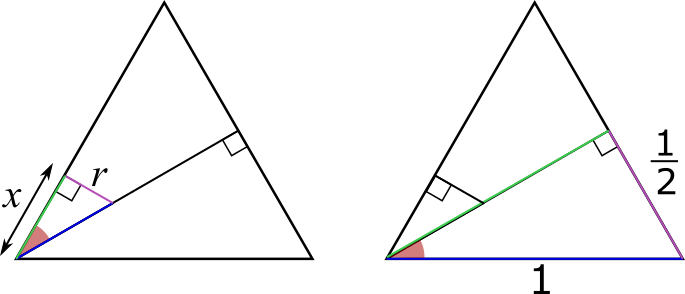
Applying Pythagoras' theorem to the larger triangle gives $\left(\frac{1}{2}\right)^2+\left(\text{green side}\right)^2=1^2$, so $\left(\text{green side}\right)^2=1-\frac{1}{4}=\frac{3}{4}$, so $\text{green side}=\frac{\sqrt{3}}{2}$.
The purple edge on the larger triangle is $\frac{1}{2}$, and it is $r$ on the smaller triangle. So the scale factor of the transformation from the larger triangle to the smaller triangle is $2r=2\times\frac{1}{2\pi}=\frac{1}{\pi}$.
So the length of the green side on the smaller triangle, $x$, is $\frac{\sqrt{3}}{2}\times\frac{1}{\pi}=\frac{\sqrt{3}}{2\pi}$.
So the circle will touch all of the perimeter of the triangle, which is 3, except for $x$ twice at each corner. So The circle will touch $3-6x=3-6\dfrac{\sqrt{3}}{2\pi}=3-\dfrac{3\sqrt{3}}{\pi}$.
