The right volume
Can you rotate a curve to make a volume of 1?
Problem
A segment of the curve $y=f(x)$ starts at $(0, 0)$ and ends at $(1, 1)$. It is rotated about the $x$ axis to form a volume. Can you find a curve which will result in a volume of $1$?
Did you know ... ?
That volumes of revolution are often used in mechanics calculations. They were used by Archimedes around 250 BC to calculate volumes of solids created by rotating conic sections about an axis.
That volumes of revolution are often used in mechanics calculations. They were used by Archimedes around 250 BC to calculate volumes of solids created by rotating conic sections about an axis.
Getting Started
Curves such as $y=x, y=x^{3/2}, y=x^{5.4}$ pass through the required points. Can you think of a more general curve to try to revolve?
Student Solutions
If we suppose that the curve $y=f(x)$ is integrable then the volume created will be
$$
V = \int^1_0 \pi y^2 dx\;.
$$
To get a feel for the sort of curve we might need, first consider the special case $y=x$, which clearly passes through the two points. Then,
$$
V = \int^1_0 \pi x^2 = \pi\left[\frac{x^3}{3}\right]^1_0 = \frac{\pi}{3}\;.
$$
This is slightly larger than $1$, so we could consider a family of curves which are beneath $y=x$.
We could look for a curve like the blue one in the diagram below:
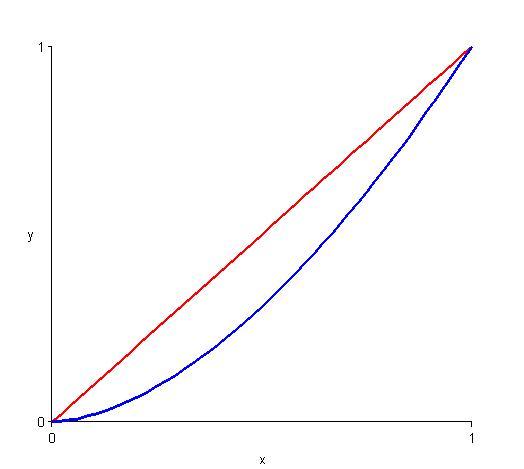
This looks like a section of a polynomial which has a root at $0$.
How about $y=x^4$?
Then,
$$
V = \int^1_0 \pi x^8 = \pi\left[\frac{x^9}{9}\right]^1_0 = \frac{\pi}{9}\;.
$$
This is still not right, but I think a polynomial could work.
Let's try $y=x^a$ where $a$ is a real number.
Then,
$$
V = \int^1_0 \pi x^{2a} = \pi\left[\frac{x^{2a+1}}{2a+1}\right]^1_0 = \frac{\pi}{2a+1}\;.
$$
If we let $a=(\pi-1)/2$ then the volume is $1$.
Therefore a solution is$$
There are, of course, others!
$$
V = \int^1_0 \pi y^2 dx\;.
$$
To get a feel for the sort of curve we might need, first consider the special case $y=x$, which clearly passes through the two points. Then,
$$
V = \int^1_0 \pi x^2 = \pi\left[\frac{x^3}{3}\right]^1_0 = \frac{\pi}{3}\;.
$$
This is slightly larger than $1$, so we could consider a family of curves which are beneath $y=x$.
We could look for a curve like the blue one in the diagram below:
Image

This looks like a section of a polynomial which has a root at $0$.
How about $y=x^4$?
Then,
$$
V = \int^1_0 \pi x^8 = \pi\left[\frac{x^9}{9}\right]^1_0 = \frac{\pi}{9}\;.
$$
This is still not right, but I think a polynomial could work.
Let's try $y=x^a$ where $a$ is a real number.
Then,
$$
V = \int^1_0 \pi x^{2a} = \pi\left[\frac{x^{2a+1}}{2a+1}\right]^1_0 = \frac{\pi}{2a+1}\;.
$$
If we let $a=(\pi-1)/2$ then the volume is $1$.
Therefore a solution is
$$
y=x^{(\pi-1)/2}\;.
$$
There are, of course, others!
