The rescaled map
Problem
Getting an Informed View
We use statistics to give ourselves an informed view on a subject of interest. This problem explores how to scale countries on a map to represent characteristics other than land area.
To see why this might be a valuable thing to do take a look at this site : https://worldmapper.org/Let's start with a simple example of a three-country continent. The countries all share a border with each other and together are surrounded by sea.
In this first view the areas of countries A, B and C are 8, 5, and 12 million sq.km
Your challenge is to complete a new view that expresses each country's population of 40, 36, and 24 million people respectively. You must retain enough of the shape and relative position for each country to be recognisable.
One way you might do this is given below - can you improve on it?
Country A has a land area of 8 million sq.km out of a total land area of 25 million sq.km, that's 32% of the land. Country A also has 40 million people from a total of 100 million, which is 40% of the total population.
That means that A needs to cover a larger area of the new map (1.25 times more to scale up from 32 to 40)
Similar calculations mean that the area of country B must scale up by 1.8 and the area of country C should be multiplied by 0.5 (half as much area)
The question now is how to apply these multipliers - here is the result of a stretching each country by its scale factor in the vertical direction (scaled version on the right).
- Can you see how this method works?
-
What are the good and bad points about this method?
- Check you can draw this and then try the same thing again but stretching instead in the horizontal direction.
-
This map was produced in Word using the Draw menu bar. If you right-click on an object you can specify the % change in either direction (look on the "size" tab)
Now back to the original challenge:
Getting Started
Student Solutions
We aim to scale the countries on the map below to represent population size.
We use the hint given and let the ocean keep its original proportion of the map, which is $\frac{39}{64}\times 100=61$ of the map.
| Country | Area (million square kilometres) | Proportion of total land area | Population (millions) | Proportion of total population |
| A | 8 | 0.32 | 40 | 0.4 |
| B | 5 | 0.2 | 36 | 0.36 |
| C | 12 | 0.48 | 24 | 0.24 |
We then find out the factors by which the country sizes need to change:
A needs to cover $\frac{0.4}{0.32}=1.25$ times more area on the map
B needs to cover $\frac{0.36}{0.2}=1.8$ times more area on the map
C needs to cover $\frac{0.24}{0.48}=0.5$ times less area on the map
So we first stretch each country by its scale factor in the vertical direction. For example, the country B would have new dimensions as below:
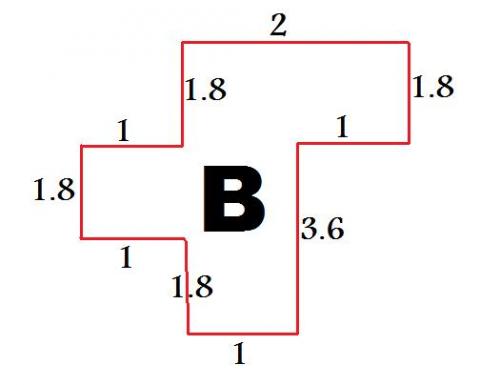
And so the overall map becomes (each square has dimensions 0.5 x 0.5)

We now scale in the horizontal direction, and for example the country C (marked in yellow) would have new dimensions as below:

And so the overall map becomes (each square again with dimensions 0.5 x 0.5)

Now we combine the scaling factors in both the horizontal and vertical directions. For example, the country A would have dimensions as below:
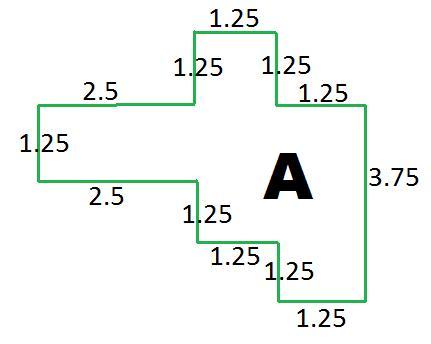
Well done to Jack from the King John School, who made a good attempt at resizing the countries in both directions. We leave this part for you to try! Perhaps scale countries B and C next, and then draw them on a map, making sure the ratio of land to ocean is kept constant.
Teachers' Resources
Hopefully students will enjoy the World Mapper images and that that will lead to discussion about the issues represented and about the process of producing images (maps) that communicate.
You may wish to draw out the different needs of map users. For example, a navigator may be concerned to have equal distances on a map matching equal distances on the real surface. Angles and bearings might be important, so that moving along a straight path on a map would correspond to taking a straight route when you travel.
Students may be encouraged to think about how maps may can be used to communicate characteristics like population density, rainfall, land under cultivation, import/export, availability of health care, etc.
That discussion would ideally include the ways in which a given method of representation plays down, or even misrepresents, certain features while giving emphasis to others.
Above all students should explore the idea that a representation is a compromise and that mathematics is used to understand the effect and scale of that compromise under different conditions.
