Rearranged Rectangle
Problem
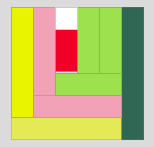
Click below to read what some other children said:
Meena:
"It's a rectangle! Or is it a square?"
Seb:
"There are lots of different coloured rectangles. They are fitted together with no gaps."
Anna:
"There is more than one of each colour rectangle."
Do you agree with each of them? Why or why not?
In fact, the picture has been made using Cuisenaire rods.
How many other, different, rectangles can you make using all of the rods that were used in the picture?
How do you know you have found them all?
You could use the interactivity below to try out your ideas if you haven't got any rods.
Getting Started
What do we mean by 'different'?
How will you make sure you don't miss out any possibilities?
Student Solutions
We had several solutions for this task.
Ella and Samuel from St Mary's Church of England Primary School in Woodbridge sent in the following:
When the blocks 1 and 2 are together it's really helpful because it's making 3. Also, if you switch the 6 block around each way then it gives you more solutions.
I found that every shape that you make you can add a really small change and you have a lot of possibilities (I haven't drawn them all as that would take forever!).
Here are four solutions from Douglas Road School in Canada:
Yiling
Juna
Mikayla
To solve the problem, I need to know what a rectangle is. A rectangle has two parallel sides from each other. A rectangle also is a quadrilateral with four sides that meet at ninety degrees angles. So that means a square counts too!
At first my method was to make as many rectangles as I could. But then I realised I made too many rectangles and their perimeters were all the same. So, my new method was to still make as many rectangles as I could but, with different perimeters.
Here are some examples of my rectangles that I think are the only ones that really count. I made 3 rectangles, including 1 square. My idea I had was thinking of the factors of 36 because 6 x 6 (which is the width and length of the original rectangle) = 36. So, the factors of 36 are 1, 2, 3, 4, 6, 12, 18 and 36.
Jasnin
In my class I did a math problem called “The Rearranged Rectangles.” The topic of the problem is “How many different rectangles can I make using the rods from the problem?”
It means I must make as many rectangles as I can using the rods from the problem. However, the area of the rectangles I made does not affect the case of the dimensions. Like if all sides are even and I made another rectangle like that, but the rods are not in same spot as the other one, it doesn't count.
It wasn't straightforward making the rectangles. But as I progressed and made big long ones, things got easier and efficient since I understood the problem more, and I got a method. My method was to try different lengths. So, if I had one rectangle with a side equal to four white rods, I would try to do another rectangle with a side equal to three white rods. The more rectangles I created with the rods, the harder it was to find different ways to make more because when you have a lot it's hard to find more.
Well done, these are excellent solutions. They do show though, that the word "different" may not mean the same thing to everyone. We have different rectangles in their length, width and perimeter. We have different rectangles according to the makeup of the cuisenaire pieces used.
Did you discuss this when you tried the task? How did you decide what 'different' means in this problem?
Teachers' Resources
Rearranged Rectangles
Talk to someone else about what you see in this picture:
Click below to read what some other children said:
Meena:
"It's a rectangle! Or is it a square?"
Seb:
"There are lots of different coloured rectangles. They are fitted together with no gaps."
Anna:
"There is more than one of each colour rectangle."
Do you agree with each of them? Why or why not?
In fact, the picture has been made using Cuisenaire rods.
How many other, different, rectangles can you make using all of the rods that were used in the picture?
How do you know you have found them all?
You could use the interactivity below to try out your ideas if you haven't got any rods.
Why do this problem?
This task gives children the chance to work systematically in a spatial and/or numerical context.Possible approach
If your children are not already familiar with Cuisenaire rods, it is essential to give them time to 'play' with the rods before having a go at this activity.Show the group the picture and invite them to talk in pairs about what they see. Take some feedback, writing up everything that is said on the board without responding, but encouraging other children to comment. Then reveal what Meena, Seb and Anna say in turn, giving time for learners to talk to their partner about whether they agree or not, and why. Use this discussion to clarify that ten 'rods' have been used to make this arrangement with no gaps, some of which are the same and some of which are different from each other. In this case, the rods form a square (which is a rectangle with equal length sides).
At this point, introduce the fact that the image was created with Cuisenaire rods and make sure that pairs of children have access to 'real' rods, or to the interactivity on a tablet or computer. Pose the challenge, "How many other, different, rectangles can you make using all the rods that were used in the picture?". Try not to give any further information at this stage and invite pairs to have a go.
As you move around the room, watch out for the different ways that learners are beginning the task. You may find that some children work in a purely geometric way, moving rods around and trying out their ideas spatially. However, others might approach the task in a numerical way by assuming that the white rod has a length of 1 unit, meaning that the area of the original square is 36 square units. They may therefore look at factor pairs of 36 and then use the rods. Neither of these approaches is better than the other (and you may well find some learners use a different method again), but you may want to stop the group and draw attention to these different ways of working. It would also be useful to have a conversation about how each pair is defining 'different'. Does 'different' in this context just mean rectangles of different dimensions? How about two rectangles of the same dimensions but made by arranging the rods in different ways and/or in different orientations?
Allow more time for pairs to work together, encouraging them to consider how they will know that they have found all the possible rectangles. In the final plenary, focus on the different ways of working systematically you have observed, whether it is in a geometrical or numerical sense, or both. You could ask learners to create a poster outlining what they have done and the conclusions they have reached to contribute to a classroom display.
Key questions
What have you done so far?How are you recording your thinking and/or your solutions?
What do we mean by 'different'?
How are you making sure you don't miss out any possibilities?
Possible support
Having access to Cuisenaire rods or the interactivity will mean that learners can try out their ideas freely, and refine their approaches, before committing anything to paper should they wish.Possible extension
Encourage learners to ask their own 'what if...?' questions and to choose one to investigate. Examples might include:- What if I take out one/two/three... of the rods, will I still be able to make rectangles?
- What if I have to have rods that are both horizontal and vertical in my rectangle?
- What if I can only arrange rods horizontally/vertically?