The property market
A property developer sells two houses, and makes a 20% loss on one and a 20% profit on the other. Overall, did he make a profit or a loss?
Problem
A property developer sells two houses, each for £252,000.
Based on the prices he paid, he made a loss of 20% on one of the houses and a profit of 20% on the other.
Overall, did he make a profit or a loss? Of how much?
Student Solutions
Answer: a loss (of £21,000)
House which made a loss: lost 20% of an original price higher than £252,000
House which made a profit: gained 20% of an original price lower than £252,000
Lost 20% of a higher number and gained 20% of a lower number $\Rightarrow$ loss overall.
This is shown in the diagram below.
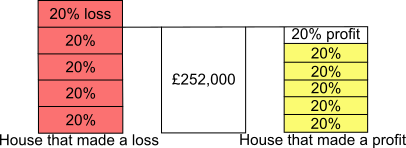
Using the diagram to find the value of the loss
Looking at the left hand side of the diagram, £252,000 is equal to 4$\times$the 20% loss.
So the loss was £252,000$\div$4 = £63,000.
Looking at the right hand side of the diagram, £252,000 is equal to 6$\times$the 20% profit.
So the profit was £252,000$\div$6 = £42,000.
So the overall loss was £63,000$-$ £42,00 = £21,000.
Using fractions to find the value of the loss
20% is the same as $\frac{1}{5}$, so the house that made a loss was sold at $\frac{4}{5}$ of its original price and the house that made a profit was sold at $\frac{6}{5}$ of its original price.
So if the house that made a loss was bought for £$L$, then $$\begin{align}252\hspace{1mm}000&=\frac{4}{5}L\\
\Rightarrow 252\hspace{1mm}\times5\div4&=L\\
\Rightarrow315\hspace{1mm}000&=L\end{align}$$
And if the house that made a profit was bought for £$P$, then $$\begin{align}252\hspace{1mm}000&=\frac{6}{5}P\\
\Rightarrow 252\hspace{1mm}\times5\div6&=P\\
\Rightarrow210\hspace{1mm}000&=P\end{align}$$
So the developer spent £315,000 + £210,000 = £525,000, and took £252,000$\times$2 = £504,000, which gives a total loss of £21,000.
Using multiplication and division to find the value of the loss
A $20\%$ price decrease corresponds to multiplying by $0.8$, so if the house that made a loss was bought for £$L$, then $L\times0.8=252\hspace{1mm}000,$ so $L=252\hspace{1mm}000\div0.8.$
A $20\%$ price increase corresponds to multiplying by $1.2$, so if the house that made a profit was bought for £$P$, then $P\times1.2=252\hspace{1mm}000,$ so $P=252\hspace{1mm}000\div1.2.$
So the total profit was $\dfrac{252\hspace{1mm}000}{0.8}+\dfrac{252\hspace{1mm}000}{1.2}-252\hspace{1mm}000\times2=-21\hspace{1mm}000$ - which is a loss of £$21,000.$
Note: writing $252,000$ as $A$ in the expression above gives a profit of $\dfrac{A}{0.8}+\dfrac{A}{1.2}-2A=A\times\left(\dfrac{1}{0.8}+\dfrac{1}{1.2}-2\right)=A\times-0.08\dot{3}$. So the loss is always $8.\dot{3}$% of the selling price of the houses.
