Polycircles

Four people cracked this one: Bella and Andaleeb from Woodhouse Sixth Form College, Sue from Madras College and Alexander from Shevah-Mofet School.

Bella started her answer by trial and error for different triangles

For the triangle of side c = 15, b = 13, a = 12:

I split the longest side (c = 15) into7 and 8, and draw 2 circles: (A, 8), that is circle with center A and radius8, and (B, 7). These 2 circles cut the 2 sides at P and Q.So CP = 13 - 8 =5 and CQ = 12 - 7 = 5. So I drew the cirle(C, 5), which just touches the other 2 cirles

Image

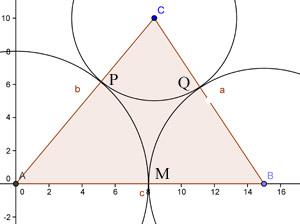
From the result above, I realize important rules to tackle the problem:

First, the difference between the 2 radii on 1 side of the triangle is equal to the difference of the 2 other sides. More specifically, AP - PC = 8 - 5 = 3 and AB - CB = 15 - 12 = 3, which means AP - PC = AB - CB. Similarlly, BQ - CQ = BA - BC = 2 and AM - MB = AC - BC = 1.

Second, the larger radius is corresponding to the larger side. For example, AB > CB. When we split AC into AP and CP, AP will be greater than CP.

These rules imply that I can always find the radii simply by splitting 1 side of the triangle such that the difference between the 2 numbers equals the difference between the 2 other sides and the larger number is corresponding to the larger side of the triangle.

I tried it out for another triangle of different size and it worked perfectly. For the triangle of side c = 10, b = 8, a = 4:

Image

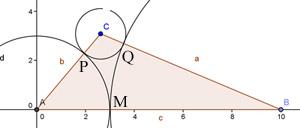
Because AB - CB = 10 - 8 = 2. I split the remaining side AC such that AP - PQ = 2. There is only the pair (1,3) which satisfy that condition. So AP = 3 and CP = 1 since AB > CB. So 3 circles are (A, 3); (B, 7); and (C, 1).

I can also prove these rules.

Assume that we can draw 3 circles which statisfy the conditions as shown by the graph

Look at the 2 sides of the triangle AB and BC:

AB = AM + BM

BC = BQ + CQ

BM = BQ

So AB - BC = AM - CQ (1)

Look at the remaining side AC:

AP = AM and CP = CQ (2)

From (1) and (2) we have:

AB - BC = AP - CP

As long as AB > BC, AP will be greater than CP

In words, this implies the rules (Q.E.D.)

Alexander sent us a more general solution.

Suppose it is possible for the triangle with sides $12$, $13$ and $15$ and the radii of the circles are $r_1$, $r_2$, $r_3$. Then

$\begin{eqnarray} \\ r_1 + r_2 &=& 12\\ r_2 + r_3 &=& 13\\ r_3 + r_1 &=& 15. \end{eqnarray}$

This set of simultaneous equations is easily solved to give $r_1 = 7$, $r_2 = 5$ and $r_3 = 8$. So we have proved that polycircles exist for this triangle.

Let's prove that it's possible for any triangle to construct circles with centres at the vertices so that the circles just touch. Let $a$, $b$ and $c$ be the sides and $r_1$, $r_2$, $r_3$ the radii of the circles. The only constraints on the radii are: $r_1> 0$, $r_2> 0$, $r_3> 0$. \begin{eqnarray} \\ r_1 + r_2 &=& a \\ r_2 + r_3 &=& b \\ r_3 + r_1 &=& c. \end{eqnarray} The solution for this system is: \begin{eqnarray} \\ r_1 &=& \frac{(a + c - b)}{2} \\ r_2 &=& \frac{(a + b - c)}{2} \\ r_3 &=& \frac{(b + c - a)}{2} \end{eqnarray} and since the sum of the lengths of any 2 sides in a triangle is bigger than the 3rd side, there are solutions for any positive $a$, $b$ and $c$.

Now consider a convex polygon with $n$ sides: $a_1$, $a_2$, $a_3$,...$a_n$. Suppose circles can be drawn with centres at the vertices of the polygon such that the circles just touch each other. Let $r_1$, $r_2$, $r_3$,... be the radii. Then: \begin{eqnarray} \\ r_1 + r_2 &=& a_1 \\ r_2 + r_3 &=& a_2 \\ ... \\ r_n + r_1 &=& a_n. \end{eqnarray} Let's try to figure out what $r_1$ equals, and all the other solutions will of course be symmetrical. \begin{eqnarray} \\ r_1 &=& a_n - r_n = a_n - a_{n-1} + r_{n-1}\\ &=& a_n - a_{n-1} + a_{n-2} - r_{n-2} = ...\\ &=& a_n - a_{n-1} + a_{n-2} - ...+(-1)^{n-1}a_1 + (-1)^nr_1. \end{eqnarray} If $n$ is even then $r_1 = a_n - a_{n-1} + a_{n-2} - ... - a_1 + r_1$ which means that the condition for the existence of solutions is: $$a_n - a_{n-1} + a_{n-2} - ... - a_1 = 0.$$ It also means that if this condition holds there are an infinite number of solutions and if it does not hold there are no solutions.

If $n$ is odd then what we get is $$r_1 = \frac{1}{2}(a_n - a_{n-1} + a_{n-2} - ... + a_1)$$ and $r_1$ is positive when $(a_n - a_{n-1} + a_{n-2} - ... + a_1) > 0.$

For polygons with an odd number of sides solutions always exist but 'negative' values of $r_i$ occur when, instead of touching externally, one circle surrounds its 'neighbour' which touches it internally so the length of the edge is given by the difference of the radii and not the sum of the radii.