Parabella
No the title is not a spelling mistake! This is a beautiful result involving a parabola and parallels. Take any two points $A$ and $B$ on the parabola $y=x^2$.
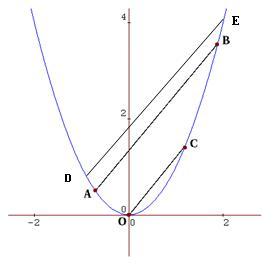
Draw the line $OC$ through the origin, parallel to $AB$ , cutting the parabola at $C$ .
Let $A=(a,a^2)$, $B= (b, b^2 )$, and $C= (c, c^2 )$. Prove that $a+b=c$.
Imagine drawing another parallel line $DE$, where $D$ and $E$ are two other points on the parabola. Extend the ideas of the previous result to prove that the midpoints of each of the three parallel lines lie on a straight line.
Biren approached it like this:
The question asks you to prove that $a+b=c$.
You already know that the two lines are parallel.This tells us that they have the same gradient.
To work out the gradients we should try to imagine we draw a right angled triangle under both lines.
We then divide the change in the $y$ direction by the change in the $x$ direction.
The change in the $x$ direction of the line $AB$ is equal to $b-a$ (small letters refer to the co-ordinates).
The change in the $y$ direction is equal to $$b^2 - a^2$$(these letters also refer to the co-ordinates).
Thus the gradient of line $AB$ is equal to: $$\frac {b^2 - a^2}{b - a} = \frac {(b-a)(b+a) }{ b-a} = b+a$$ The change in the $y$ direction of the line $OC$ is $c^2$ The change in the $x$ direction is equal to $c$. Thus the gradient of the line $OC$ is $$\frac {c^2}{c} = c$$
We know that both lines, $AB$ and $OC$ are parallel, and so they must have the same gradient.
So $b+a = c$
Image
|
Alex extended the result as follows: Let $d$ and $e$ be the $x$ coordinates of D and E
respectively. As OC is parallel to DE, the relationship of OC to DE
is the same as it was to AB, therefore $c=d+e$ just as $c=a+b$. The
$x$ coordinates of the midpoints of AB, DE and OC and all the same,
because
$$\frac{(a+b)}{2 }= \frac{(d+e)}{2} = \frac{c}{2}.$$ The
straight line $x = \frac {c}{2}$ passes through the midpoints of
all the parallel lines.
|
Others approached the problem in a slightly different way:
Let $y = mx + n$ be the equation of the line going through the points $A(a, a^2 )$ and $B(b, b^2 )$.
At $A$, $a^2 = ma + n$
At $B$, $b^2 = mb + n$
From this: $$a^2 - b^2 = ma - mb = m (a - b).$$ Dividing by $(a-b)$: $$m = \frac {a^2 - b^2}{a - b} = \frac {(a + b)(a - b)}{a - b} = a + b$$ The line $OC$ passes through the origin and the point $C(c, c^2 )$.
Because it passes through the origin, its equation is of the form: $$y = ux$$ Because it is parallel to the line passing through $A$ and $B$, $u = m$, so its equation is: $$y = (a + b)x$$ Since it passes through $C$: $$c^2 = (a + b)c$$ or: $$c = a + b.$$
Why do this problem?
This is a quick, simple problem on gradients with a neat result. It will help to reinforce ideas about lines and coordinate geometry and factorising expressions.
Possible approach
Key question
Possible extension
Possible support
Just do the first part of the problem.