Number daisy
Problem
Number Daisy printable worksheet
| 1 = 1 2 = 2 3 = 1 + 2 4 = 4 5 = 5 6 = 2 + 4 7 = 1 + 2 + 4 8 = 5 + 1 + 2 9 = 4 + 5 10 = 7 + 1 + 2 11 = 5 + 4 + 2 12 = 5 + 4 + 2 + 1 13 = 7 + 6 14 = 7 + 6 + 1 15 = 7 + 6 + 2 16 = 7 + 6 + 2 + 1 17 = 7 + 5 + 4 + 1 18 = 7 + 5 + 4 + 2 19 = 7 + 5 + 4 + 2 + 1 20 = 5 + 7 + 6 + 2 21 = 5 + 7 + 6 + 2 + 1 22 = 4 + 5 + 7 + 6 23 = 5 + 7 + 6 + 1 + 4 24 = 5 + 7 + 6 + 2 + 4 25 = 5 + 7 + 6 + 2 + 4 + 1 |
This Daisy is special because you can make every number from 1 to 25. You are only allowed to add neighbours (numbers touching each other) and you can only use each number once in a sum. |
Image
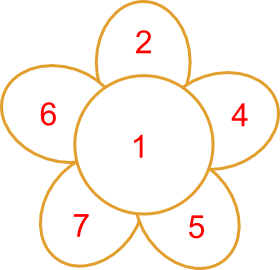
|
We can make all the numbers from 1 to 25 using this Daisy.
Can you do better than this with a different set of numbers?
The challenge is to find six numbers to go in the Daisy from which you can make all the numbers from 1 to a number bigger than 25.
This task was found in one of Brian Bolt's books and developed by MEDIAN in their collection of interesting number resources.
Student Solutions
We received lots of excellent solutions to this problem. Well done to students from Raines School, Lancaster Lane School, Risley Primary School, Garden International School, Glan-Y-Mor, Selside School, Kings School, Beijing City International School, Cirencester Kingshill School, Highfields School, Winster C of E School and Balfour Junior School for all finding solutions which give numbers greater than 25.
Alison managed to find numbers 1 to 46 with this daisy: 1 in centre, 2,4,12,19,8 around the edge.
Ria's method for making a daisy with numbers 1 to 28 can be found here.
Simon and Will made a daisy with numbers 1 to 37 and explain their method below:
To begin, we used the same flower as NRICH. We put 1 in the middle because we decided that it would be the most used number. We put 2 in next to make 2 and 3. Then we put a 4 in and we could make numbers 5,6,7. We wrote the numbers we could make underneath the flower. We then added 8 to make 8,9,10. We put 8 next to the 2 and we then could make numbers up to 15. We then added 12 and put it next to the 4 to make 16. The 10 was the last number to be added. We added 8 + 10 + 12 + 4 + 2 + 1 to make the biggest number 37. We then tried to make all the numbers in between and it worked.
Here are some more solutions.
Emma's daisy makes all the numbers 1 to 38:

Tamsin's daisy makes all the numbers from 1 to 40:

Carolyn's daisy makes all the numbers from 1 to 43:

Stephen's daisy makes all the numbers from 1 to 45:

Students from Riccarton High School found another daisy that makes all the numbers from 1 to 45:

They checked this worked by entering the six numbers in the cells of a spreadsheet and reproduced the numbers in six columns with the total on the right. It was then necessary to go through deleting some numbers on each line to give the totals 1 to 45 as in Ali's solution below:
| 1 | 21 | 8 | 9 | 2 | 4 | Total |
| 1 | 1 | |||||
| 2 | 2 | |||||
| 1 | 2 | 3 | ||||
| 4 | 4 | |||||
| 1 | 4 | 5 | ||||
| 2 | 4 | 6 | ||||
| 1 | 2 | 4 | 7 | |||
| 8 | 8 | |||||
| 1 | 8 | 9 | ||||
| 9 | 10 | |||||
| 9 | 2 | 11 | ||||
| 1 | 9 | 2 | 12 | |||
| 1 | 8 | 4 | 13 | |||
| 1 | 9 | 4 | 14 | |||
| 9 | 2 | 4 | 15 | |||
| 1 | 9 | 2 | 4 | 16 | ||
| 8 | 9 | 17 | ||||
| 1 | 8 | 9 | 18 | |||
| 8 | 9 | 2 | 19 | |||
| 1 | 8 | 9 | 2 | 20 | ||
| 21 | 21 | |||||
| 1 | 21 | 22 | ||||
| 21 | 2 | 23 | ||||
| 1 | 21 | 2 | 24 | |||
| 21 | 4 | 25 | ||||
| 1 | 21 | 4 | 26 | |||
| 21 | 2 | 4 | 27 | |||
| 1 | 21 | 2 | 4 | 28 | ||
| 21 | 8 | 29 | ||||
| 21 | 9 | 30 | ||||
| 1 | 21 | 9 | 31 | |||
| 21 | 9 | 2 | 32 | |||
| 1 | 21 | 9 | 2 | 33 | ||
| 1 | 21 | 8 | 4 | 34 | ||
| 1 | 21 | 9 | 4 | 35 | ||
| 21 | 9 | 2 | 4 | 36 | ||
| 1 | 21 | 9 | 2 | 4 | 37 | |
| 21 | 8 | 9 | 38 | |||
| 1 | 21 | 8 | 9 | 39 | ||
| 21 | 8 | 9 | 2 | 40 | ||
| 1 | 21 | 8 | 9 | 2 | 41 | |
| 21 | 8 | 9 | 4 | 42 | ||
| 1 | 21 | 8 | 9 | 4 | 43 | |
| 21 | 8 | 9 | 2 | 4 | 44 | |
| 1 | 21 | 8 | 9 | 2 | 4 | 45 |
Teachers' Resources
This printable worksheet may be useful: Number Daisy.
Why do this problem?
This problem builds fluency in numerical manipulation and encourages independent investigation and systematic working. The activity is very accessible but leads into interesting questions about number properties and number bonds.
Possible approach
You could explain the concept of a Number Daisy and demonstrate how to find a selection of numbers using the daisy. Working in pairs or individually, the students could then find the remaining totals to check that the numbers 1 to 25 really can all be made.
Using mini-whiteboards and squared paper (to allow students to draw a table to record their results systematically) might be useful in this activity. Let students choose numbers and arrange them on their daisies. Challenge them to find a daisy that can make the most numbers.
Allow groups to check each others’ daisies and give them time to describe their strategies. Towards the end, have a class discussion to exchange ideas and strategies, and to see who in the class got the highest total.
Key questions
How can we record our findings?
Are there some numbers you will always need?
Are some numbers more useful than others?
What do you notice about the number that is in the middle of the daisy?
Why is the layout of the numbers important?
Possible support
You could start by only using numbers between 1 and 9.
You could relax the rule that only neighbouring numbers can be added.
Possible extension
What happens if we change the layout of the numbers?
What happens if we have a different number of petals?
What happens if we are allowed to subtract as well as add?
