More Dicey Decisions

The twelve edge totals of a standard six-sided die are distributed symmetrically. Will the same symmetry emerge with a dodecahedral die?

Age

16 to 18

Challenge level

Exploring and noticing Working systematically Conjecturing and generalising Visualising and representing Reasoning, convincing and proving

Being curious Being resourceful Being resilient Being collaborative

Problem

In the problem Dicey Decisions, we encouraged you to consider the possible edge totals by adding up the numbers that meet on the different edges of a six-sided die.

If you haven't already done this, why not try now?

Imagine that instead of a six-sided die we had a dodecahedron numbered 1-12.

There are different ways to arrange the numbers from 1-12. A standard six-sided die has opposite faces that sum to 7, so perhaps our dodecahedral die should have opposite faces that sum to 13.

Can you create a net for a dodecahedral die whose opposite faces sum to 13?

For the six-sided die, the edge totals were distributed like this:

Edge total	3	4	5	6	7	8	9	10	11
Frequency	1	1	2	2	0	2	2	1	1

The mean edge total is 7, and the edge totals are distributed symmetrically about the mean.

What is the mean edge total for your dodecahedral die?

Are the edge totals distributed symmetrically?

Ignoring rotations and reflections, there is only one way to number a cube to create a six-sided die with the constraint that opposite faces sum to 7, but there are multiple ways to create a dodecahedral die with opposite faces that sum to 13.

Can you make any general statements about which dodecahedral dice will have edge totals with a symmetric distribution? Can you prove your statements?

For the six-sided die, the corner totals were also distributed symmetrically. Will the same be true for the corner totals of a dodecahedral die?

Now use your insights to make and justify some statements about the edge and corner totals of an icosahedral (20-sided) die with opposite faces that sum to 21.

Student Solutions

Here's an example of a net for a dodecahedral die with the opposite numbers summing to 13:

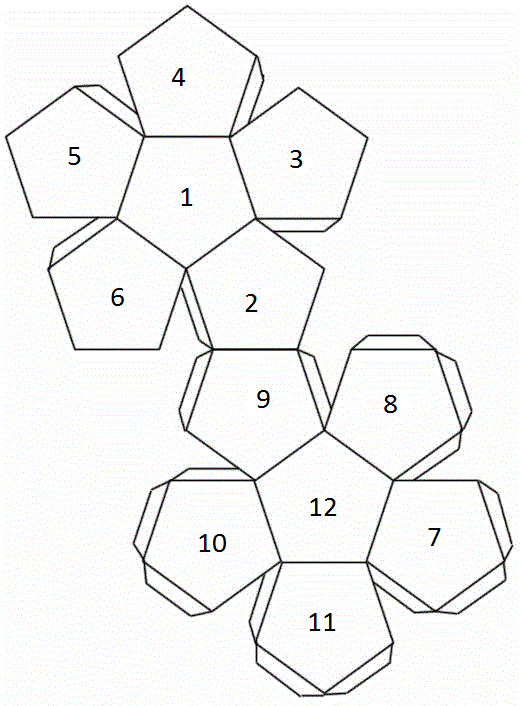
For such a dodecahedral die with the numbers 2,3,4,5,6 around 1, and opposite faces summing to 13, the edge totals are:

Edge 1	Edge 2	Sum	Edge 1	Edge 2	Sum
1	2	3	1	3	4
1	4	5	1	5	6
1	6	7	2	3	5
2	6	8	2	9	11
2	8	10	3	4	7
3	4	7	3	8	11
3	7	10	4	5	9
4	7	11	4	11	15
5	6	11	5	11	16
5	10	15	6	10	16
6	9	15	9	8	17
9	10	19	9	12	21
8	7	15	8	12	20
7	11	18	7	12	19
11	10	21	11	12	23

If we plot the frequency distribution for the possible scores for this die we get:

Score	Frequency	Score	Frequency
3	1	13	0
4	1	14	0
5	2	15	4
6	1	16	2
7	2	17	1
8	1	18	1
9	1	19	2
10	2	20	1
11	4	21	2
12	0	22	1
		23	1

This is a symmetric distribution with a mean score of 13. It turns out all possible dodecahedral dice with faces summing to 13 have this property. Consider swapping two of the faces, say 2 and 3, which will also swap 11 and 10 on the opposite side of the die. The sum of the edge between 2 and 3, and 11 and 10 will stay the same, however the other edges of these faces will either increase or decrease by 1. The edge between faces A and B, say, will change in the opposite direction to the edge between the faces (13-A) and (13-B), as if A, say, increases by 1, (13-A) will decrease by 1. It follows from this that the distribution of the row sums will remain symmetric.

In general, you can prove that swapping two arbitrary faces can be done as the product of swapping pairs of adjacent faces, and as we've just shown the simpler process of just swapping one pair of faces leaves the distribution symmetric, we've therefore shown that all swaps will.

For our example, we have the corner sums:

Faces	Sum	Faces	Sum	Faces	Sum	Faces	Sum
1,2,3	6	2,3,8	13	4,5,11	20	7,8,12	27
1,3,4	8	2,6,9	17	4,7,11	22	7,11,12	30
1,4,5	10	2,8,9	19	5,6,10	21	8,9,12	29
1,2,6	9	3,4,7	14	5,10,11	26	9,10,12	31
1,5,6	12	3,7,8	18	6,9,10	25	10,11,12	33

These have an average of 19.5, and are also symmetrically distributed about that point. The same argument given for the edges remaining symmetric under the exchange of faces can be adapted to prove the claim that the corner sums remain symmetrically distributed when pairs of faces are swapped.

The important fact throughout these arguments is that the opposite faces always add up to 13. If this wasn't the case, then the distribution would not remain symmetric under the swapping of all pairs of faces.

Teachers' Resources

Why do this problem?

This problem offers students the opportunity to consider the symmetry of dodecahedra, and to develop insights from reasoning about dodecahedra to help them to analyse symmetry in icosahedra.

Possible approach

This problem follows on from Dicey Decisions.

The problem could be given to students to work on independently (perhaps as a homework task) but could also be used as a whole class activity as follows:

Start by making sure students are happy with the idea that opposite faces of a six-sided die sum to 7, and then challenge them to come up with a dodecahedral die where the opposite faces sum to 13. Some students may wish to visualise the die, some may be happy working with a two-dimensional representation, and some may prefer to create a net and actually make the die in three dimensions.

There is opportunity for rich discussion about the number of distinct dodecahedral dice it is possible to make (with the constraint that opposite faces sum to 13), and different groups of students could be encouraged to work with distinct dice.

Once students have created (or visualised) their die, ask them to create a frequency table showing the frequency with which the different edge scores occur.

"Does everyone get a symmetric distribution?"

"Are you surprised that everyone got a symmetric distribution even if they started with different dice?"

"Can you explain why it was symmetric?"

This could lead into rich discussion about the symmetry of the distribution and how it relates to the constraint that opposite faces sum to 13.

Finally, once students have explanations of where the symmetry in the distribution comes from, they could be challenged to do a similar analysis for corner totals of the dodecahedral die, or for edges or corner totals on an icosahedral die.

Key questions

If a face of the die is numbered $n$, what would the opposite face be numbered?

If adjacent faces were numbered $n$ and $m$ (with an edge total between them of $n+m$, what would the opposite edge total be?

Possible extension

Write up a really clear proof of the result concerning the symmetric distribution of the edge totals.

I have a 100-sided die. To the eye, it looks pretty regular, but it can't be exactly regular because there is no such thing as a 100 sided Platonic solid. Consider the issues which might arise in an analysis of the various totals.

Possible support

Spend time considering the edge totals of the six-sided die to make sense of the symmetry there before working on the dodecahedron.

Or search by topic

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners