Luis' Eight
Luis writes down eight consecutive positive integers. The sum of the three smallest numbers is 33. What is the sum of the three largest numbers?
Problem
Luis writes down eight consecutive positive integers.
The sum of the three smallest numbers is $33$.
What is the sum of the three largest numbers?
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Student Solutions
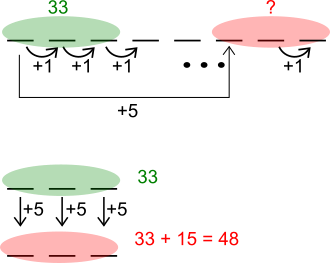
Answer: $48$
Using symbols
Luis' numbers: $n$, $n+1$, $n+2$, $n+3$, $n+4$, $n+5$, $n+6$ and $n+7$
The sum of the three smallest numbers: $n+(n+1)+(n+2) = 3n+3$
The sum of the three largest numbers: $(n+5)+(n+6)+(n+7) = 3n+18$
Three smallest numbers add up to $33$ so $3n+3 = 33$
$3n+18 = (3n+ 3) + 15 = 33+15 = 48$
Alternatively method using symbols:
Luis' numbers: $n$, $n+1$, $n+2$, $n+3$, $n+4$, $n+5$, $n+6$ and $n+7$
The sum of the three smallest numbers: $n+(n+1)+(n+2) = 3n+3$
Three smallest numbers add up to $33$, so $3n+3 = 33$, so $n = 10$
So Luis' numbers are: $10$, $11$, $12$, $13$, $14$, $15$, $16$ and $17$
The sum of the three largest numbers: $15+16+17 = 48$
Thinking about patterns in the numbers:
