LOGO challenge 10 - circles
In LOGO circles can be described in terms of polygons with an infinite (in this case large number) of sides - investigate this definition further.
Problem
These challenges arose from conversations and ideas during a Royal Institution Saturday morning Maths Workshop. Consider the procedure:
TO POLY :X :Y
REPEAT :Y [FD :X LT 360/:Y]
END
where :X and :Y are variables, that can be changed as you experiment and try to understand what is happening.
Think about, try to imagine, then experiment with:
POLY 50 7
POLY 20 16
POLY 20 30
etc..
What happens as the value for :Y increases yet further? (i.e. considering the limitations with your monitor's powers of resolution.)
.
.
.
BUT
.
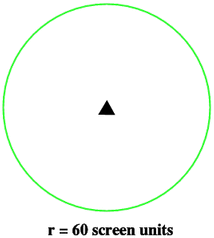
What is the most elegant way of coding the drawing of a circle of radius 60 screen units in the centre of your screen?
[Hint: use the primitive HOME to return turtle.]
Naturally, geometric designs have long been embellished with circles.
You might like to consider re-creating the following designs this month.
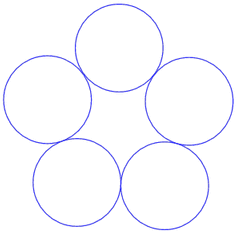
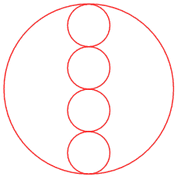
Teachers' Resources
