Integers on a Sphere
Can you find all the integer coordinates on a sphere of radius 3?
Problem
A sphere of radius 3 has its centre at the origin.
How many points on the surface of the sphere have coordinates that are all integers?
This problem is taken from the UKMT Mathematical Challenges.
Student Solutions
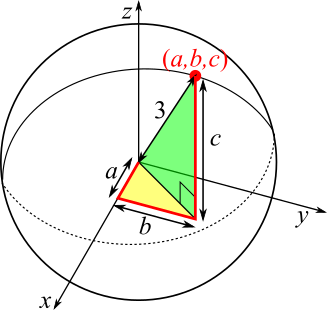
Consider a point $(a,b,c)$ on the sphere, as shown in the diagram.
The yellow and green triangles are both right-angled, and the hypotenuse of the yellow triangle is one of the sides of the green triangle. Let this side be $k$. All of the other sides of the triangles are known in terms of $a$, $b$ and $c$, so we can make an expression linking $a$, $b$ and $c$ by applying Pythagoras' Theorem to the two triangles.
Yellow triangle: $a^2+b^2=k^2$
Green triangle: $k^2+c^2=3^2\Rightarrow a^2+b^2+c^2=9$
Since $a$, $b$ and $c$ are integers, $a^2$, $b^2$ and $c^2$ must be $0$, $1$, $4$ or $9$. Choosing $a^2$ first, and then $b^2$ so that $a^2+b^2\le9$, and then $c^2$ so that $a^2+b^2+c^2=9$, the possible options are shown in this table.
| $a^2$ | $b^2$ | $c^2$ |
|---|---|---|
| $0$ | $0$ $1$ $4$ $9$ | $9$ $8$ not possible $5$ not possible $0$ |
| $1$ | $0$ $1$ $4$ | $8$ not possible $7$ not possible $4$ |
| $4$ | $0$ $1$ $4$ | $5$ not possible $4$ $1$ |
| $9$ | $0$ | $0$ |
That gives $6$ possible options for $a^2$, $b^2$ and $c^2$.
For $0,0,9$ and so on, $a$, $b$ and $c$ are $0$, $0$ and either $+3$ or $-3$ in some order. So for the $3$ options that are made up of two $0$s and a $9$, there are $3\times2=6$ integer points on the sphere.
For an option such as $4$, $4$, $1$, we could have $(2,2,1)$, $(2,2,-1)$, $(2,-2,1),$ $(2,-2,-1)$, $(-2,2,1)$, $(-2,2,-1)$, $(-2,-2,1),$ $(-2,-2,-1)$ - which gives $8$ integer points. So for the $3$ options that are made up of two $4$s and a $1$, there are $3\times8=24$ integer points on the sphere.
That gives a total of $6+24=30$ integer points on the sphere.
