Height and sides
Can you find the area of the triangle from its height and two sides?
Age
14 to 16
Challenge level
Problem
Imagine you have an acute-angled triangle.
The lengths of two of the sides, and the perpendicular height from the third side, are 12, 13 and 15, but not necessarily in that order.
What is the area of the triangle?
This problem is taken from the UKMT Mathematical Challenges.
Student Solutions
The diagram below shows the lengths given. Clearly the perpendicular height is the shortest of the lengths so must be $12$.
Image
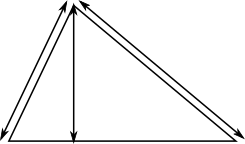
We then have two right-angled triangles. In both cases, the base can be found using Pythagoras' theorem, and then the area can be found from $\frac{1}{2}\text{base}\times\text{height.}$
Image
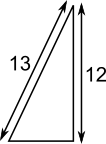
$$\begin{align}\text{base}^2+12^2=&13^2\\
\Rightarrow \text{base}^2+144=&169\\
\Rightarrow \text{base}^2=&169-144=25\\
\Rightarrow\text{base}=&5\end{align}$$ $$\text{area}=\frac12\times5\times12=30$$
Image
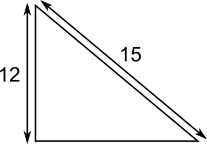
\Rightarrow \text{base}^2+144=&225\\
\Rightarrow \text{base}^2=&225-144=81\\
\Rightarrow\text{base}=&9\end{align}$$ $$\text{area}=\frac12\times9\times12=54$$
So the total area is $30+54=84$.