Green Cube, Yellow Cube
Problem
There are eight small cubes. Each face of each cube is to be painted either green or yellow but each cube must use each of the two colours somehow.
Work out how to paint the faces so that the cubes can be put together to make a $2$ by $2$ by $2$ cube that is green all over AND can be rearranged to make a $2$ by $2$ by $2$ cube that is yellow all over.
Now work out how to paint the faces to make a $3$ by $3$ by $3$ green cube and a $3$ by $3$ by $3$ yellow cube.
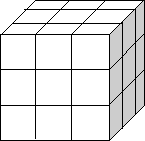
Student Solutions
For the $2$ by $2$ cube
Idil (Private IRMAK Primary & Secondary School, Istanbul, Turkey) says:
Jason (Priory School UK), Christina (Malborough Primary School, UK), and Dogan (Private IRMAK Primary & Secondary School, Istanbul, Turkey) drew a net of a cube to show the colour of each face.
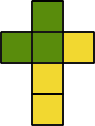
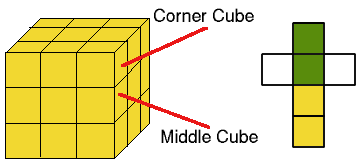
For the $3$ by $3$ cube
Dogan Private IRMAK Primary & Secondary School, Istanbul, Turkey) explains that:
We can paint corners the same as we did before. Then we can paint cubes in the middle like two sides yellow, two sides green - you don't need to paint the other sides. The following figure shows an opened middle cube and how it should be painted:
Teachers' Resources
Green Cube, Yellow Cube
There are eight small cubes. Each face of each cube is to be painted either green or yellow but each cube must use each of the two colours somehow.
Work out how to paint the faces so that the cubes can be put together to make a $2$ by $2$ cube that is green all over AND can be rearranged to make a $2$ by $2$ cube that is yellow all over.
Now work out how to paint the faces to make a $3$ by $3$ green cube and a $3$ by $3$ yellow cube.
Why do this problem?
Possible approach
Key questions
Possible extension
