Fraction of percentages
What is $W$ as a fraction of $Z?$
Problem
The value of $W$ is $25\%$ of $X$.
The value of $X$ is $45\%$ of $Y$.
The value of $Z$ is $60\%$ of $Y$.
What is $W$ as a fraction of $Z?$
This problem is taken from the World Mathematics Championships
Student Solutions
Answer: $\frac3{16}$
Using fractions
$W$ is $25\%$ of $X$, which is $\frac14$ of $X$
$X$ is $45\%$ of $Y$, so $X=\frac9{20}Y$
$Z$ is $60\%$ of $Y$, so $Z=\frac35Y$
$$\begin{align}
W&=\tfrac14X\\
&=\tfrac14\left(\tfrac9{20}Y\right)\\
&=\tfrac9{80}Y\end{align}$$
$Z=\frac35Y$ and so $Y=\frac53Z$
$$\begin{align} \tfrac9{80}Y&=\tfrac9{80}\left(\tfrac53Z\right)\\
&=\tfrac3{16}Z\end{align}$$
Using $100$ parts of $Y$
Suppose $Y$ is split into $100$ parts, so that each part is $1\%$ of $Y$.
Then $Z$ is $60\%$ of $Y$ so $Z$ is $60$ parts, and $X$ is $45$ parts.
So $50\%$ of $X$ would be half of $45$ parts, which is $22.5$ parts, and $25\%$ of $X$, which is $W$, is half of $22.5$ parts. Half of $22.5$ is $11.25$, so $W=11.25$ parts.
Then $\frac{W}{Z}=\frac{11.25}{60}$
Multiplying the numerator and denominator by $4$ to get whole numbers gives $\frac{W}{Z}=\frac{45}{240}$ which simplifies $\frac{45}{240}=\frac{9}{48}=\frac{3}{16}$.
Using a diagram (and fractions)
$60\%$ and $45\%$ can both be easily represented by splitting the whole into $20$ pieces, as shown in the diagram below. Beginning by splitting $Y$ into $20$ pieces, $Z$ is $60\%$ of $Y$ so $12$ pieces (since $60\%$ is the same as $\frac6{10}$ or $\frac{12}{20}$) and $X$ is $45\%$ of $Y$ so $9$ pieces (since $45\%$ is halfway between $\frac4{10}$ and $\frac5{10}$, so halfway between $\frac8{20}$ and $\frac{10}{20}$, which is $\frac9{20}$).
$W$ is $25\%$ of $X$, which is the same as $\frac14$ of $X$. $X$ is made up of $9$ pieces, so it is difficult to find $\frac{1}{4}$ of $X$ as $9$ is not divisible by $4$.
By splitting each of the $9$ pieces into $4$ smaller pieces, $X$ will be represented as $9\times4=36$ smaller pieces, and $W$ is the same as $9$ of these smaller pieces, as shown below.
To compare $Z$ and $W$, we should also split each of the $12$ pieces of $Z$ into $4$ smaller pieces, so that the pieces in $Z$ are the same size as the pieces in $W$. That means $Z$ will be made up of $12\times4=48$ small pieces, as shown at the bottom of the diagram.
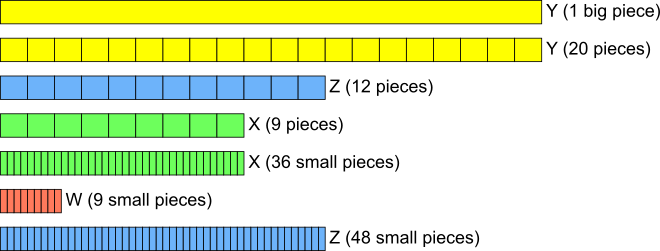
So $\frac{W}{Z}=\frac{9}{48}$, which simplifies to $\frac{3}{16}$ (by dividing numerator and denominator by $3$).
Using percentages
$W$ is $25\%$ of $X$, which is $45\%$ of $Y$, so $W$ is $25\%$ of $45\%$ of $Y$.
$Z$ is $60\%$ of $Y$. So $\frac{W}{Z}=\dfrac{25\%\times45\%\times Y}{60\%\times Y}=\dfrac{25\%\times45\%}{60\%}$.
Writing the percentages as fractions over $100$, this is equal to $$\begin{split}\frac{\frac{25}{100}\times\frac{45}{100}}{\frac{60}{100}}&=\frac{25\times\frac{45}{100}}{60}\\ \hspace{1mm}\\
&=\frac{25\times45}{60\times100}\\ \hspace{1mm}\\
&=\frac{25\times9\times5}{12\times5\times 25\times4}\\ \hspace{1mm}\\
&=\frac{9}{12\times4}\\ \hspace{1mm}\\
&=\frac{3\times3}{3\times4\times4}\\ \hspace{1mm}\\
&=\frac{3}{16}\end{split}$$
