Divisible factorisations

Factorise $n^{5}-n^{3},$ and show that it is divisible by $24.$

Nishad from Thomas Estley Community College, Dylan from Brooke Weston, Alex from Stowe School and Ishaan from Simon Balle All-Through School, all in the UK, used arguments about consecutive and even numbers. This is Dylan's work (there is one very minor error at the end, which is corrected):

Image

Prem from Cranford Community College, Pratyush from Wilson's School, Ziwei (Gilbert) from Stowe School and Deeya from Winstanley College Wigan, all in the UK, and Natal from Canada used algebra to check that $n^5-n^3$ is divisible by $8$ whether $n$ is odd or even. This is Deeya's work:

Image

Prove that $2^{2n}-1$ is divisible by $3$.

Harris from Stowe School and Nishad noticed a pattern in the powers of $2.$ Harris wrote:

Image

Nishad, Ziwei (Gilbert), Pratyush and Ishaan factorised the expression to prove what Harris noticed. This is Ishaan's work:

Image

Pratyush used a binomial expansion to prove the statement:

Image

Prem, Dylan, Alex and Natal used induction to prove the statement. This is Prem's work:

This proof can be done quite nicely via induction (a rather lovely tool). First, we assume a base case - for this question, our base case is $n=1$ since our statement holds for all positive integers. We can then attempt to prove our base case which is rather simple for this question. $2^{2(1)} − 1 = 3$ (which is divisible by $3$).

Now, we take a rather bold move where we assume that $3 | 2^{2k}−1$ for some $k \in\mathbb{N}\Rightarrow 2^{2k}−1 = 3q$ for some $q \in \mathbb{N}$. The notation may look intimidating at first if you haven’t seen it before but all it says that the $2^{2k}− 1$ is divisible by $3$ which means it can be written as $3q$ where $q$ is an integer.

This may seem pointless at fist but it will be helpful when analyse the next case for $n = k + 1,$ $2^{2( k+1)} − 1.$ We can use the law of indices to help re write our expression as $2^2 · 2^k − 1.$ Now, we simply factor out a $4$ but naturally you may be scared to do so because we can’t easily pull out a $4$ from that $−1$ can we? Well say we did anyways, and we had $4(2^k − 1)$ and we expanded it all out, we’d get $4 · 2^k − 4$ which is almost what we had before! Ah-ha, you might notice all we have to do is add three and we get back what we had. So, for $n = k+1$ we get $4(2^k−1)+3.$

This is where the magic happens. Remember that almost random step we did in the 2nd paragrah - well look inside that bracket, it’s our case for $n = k$ so we can rewrite it again as $4(3q) + 3$ which is simply $3(4q + 1).$

This is when we have to use some logic, if we proved the statement to be true for $n = 1$ and we assumed it to be true for $n = k$ and using that result we proved that it’s true for $n = k + 1$ then it must be true $\forall n \in \mathbb N$

Natal used the same principle but a different algebraic method:

Image

Notice that Natal's method not only proves that $2^{2n}-1$ is divisible by $3$ for all positive integers $n,$ but also what Nishad and Harris noticed: even powers of $2$ are one more than a multiple of $3,$ but odd powers of $2$ are one less than a multiple of $3.$

Nishad proved the statement in another way, using modular arithmetic. Nishad uses "$\equiv a (\mod3)$" to mean "leaves a remainder of $a$ when divided by $3$"

Image

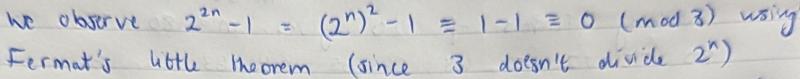
Nishad has not actually used Fermat's Little Theorem. Since $3$ doesn't divide $2^n,$ $2^n$ has a remainder of $1$ or $2$ when divided by $3.$ Working with remainders when divided by $3,$ squaring the remainder of $1$ or $2$ will always give a remainder of $1$ when divided by $3.$

This is because $(3p+2)^2 = \underbrace{(3p)^2+ 2\times(3p)\times2}_\text{multiple of 3}+2^2=3q+4=3r+1$

(and similarly for $(3p+1)^2$ - the $1^2$ is the only part that is not automatically a multiple of $3$).

So $\left(2^n\right)^2$ has remainder $1$ when divided by $3,$ and so $\left(2^n\right)^2-1$ is a multiple of $3.$

If $n-1$ is divisible by $3$, show that $n^{3}-1$ is divisible by $9$.

Nishad, Dylan, Alex and Harris showed this algebraically, by factorising the difference of two cubes. This is Alex's work:

Image

Prem, Rishik K, Ishaan and Natal used the same idea but without factorising as the difference of two cubes. This is Rishik's work:

$n – 1 = 3x, $  $x$ represents any number to indicate that $n-1$ is divisible by $3.$

Making $n$ the subject of the formula:

$n = 3x + 1$

$n^3 = (3x+1)^3$

$n^3 = 27x^3 + 27x^2 + 9x + 1$

$n^3 – 1 = 27x^3 + 27x^2 + 9x$

This expression is divisible by $9$ because if I divide this by expression, I will obtain the result:

$3x^3 + 3x^2 + x$

Therefore, $n^3 − 1$ is divisible by $9.$

 

Ziwei (Gilbert) worked in terms of $n$ and considered what factors each expression had:

Image

Nishad used modular arithmetic, like before, to prove the statement very neatly. Below the proof using modular arithmetic, Nishad repeats the proof without using modular arithmetic:

Image