Distance to the corner
Can you find the distance from the well to the fourth corner, given the distance from the well to the first three corners?
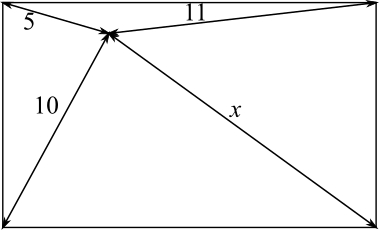
Problem
A well is dug in a courtyard. The distances from the well to three of the corners are 10 metres, 5 metres and 11 metres, as shown in the diagram below.
Find the distance from the well to the fourth corner.
Image
Student Solutions
Labelling horizontal and vertical distances using letters
Drawing on vertical and horizontal distances from the well to the corners and labelling them $a,b,c$ and $d$ gives the image below.
Image
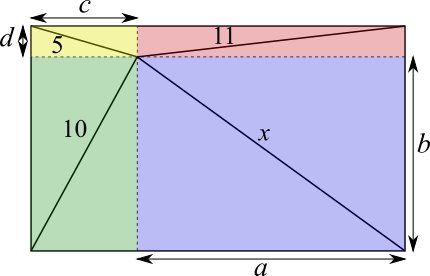
From the blue rectangle, $a^2+b^2=x^2$.
From the green rectangle, $b^2+c^2=100$.
From the red rectangle, $a^2+d^2=121$.
From the yellow rectangle, $c^2+d^2=25$.
Adding the equations given by the green and red rectangles gives $$\begin{align}b^2+c^2+a^2+d^2=&100+121\\ \Rightarrow \left(a^2+b^2\right)+\left(c^2+d^2\right)=&221\end{align}$$ And now substituting $a^2+b^2=x^2$ and $c^2+d^2=25$ gives $$\begin{align}&x^2+25=221\\ \Rightarrow&x^2=196\\ \Rightarrow &x=14\end{align}$$
Using a diagram
In the diagram below, the courtyard has been split into 4 rectangles whose corners are at the well. The squares drawn on are for the diagrammatic representation of Pythagoras' theorem, so that the area of shaded square A added to the area of shaded square B is equal to $x^2$, because $x$ is the hypotenuse of the triangle in the blue rectangle.
Image
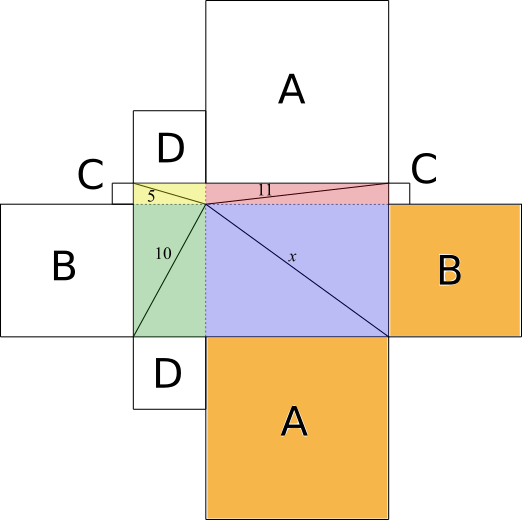
Without using the blue rectangle, how else can we get A+B?
The square of the hypotenuse in the red rectangle is A+C, and the square of the green rectangle is B+D. Adding these together gives A+B+C+D, which is too much by C+D. But the square of the hypotenuse in the yellow rectangle is C+D.
So A+B=11$^2$+10$^2-$5$^2$=196.
So $x^2$ = 196, so $x$ = 14.
Using vectors and the scalar product
In the diagram below, the vectors from the well to the four corners of the rectangle are labelled $\bf{a,b,c}$ and $\bf{x}$.
Image
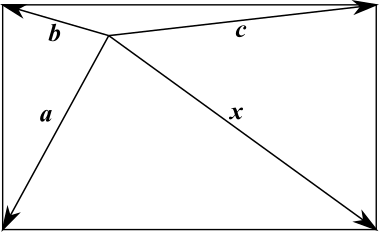
From the diagram below, it can be seen that the vector $\bf{x}$ is equal to $\bf{a}+\bf{c}-\bf{b}$, and that the sides of the rectangle can be written as $\bf{b}-\bf{a}$ and $\bf{c}-\bf{b}$.
Image
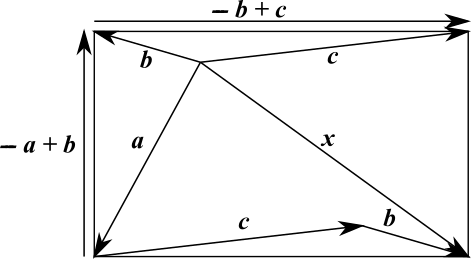
The sides of the rectangle are perpendicular, so $$\begin{align}\left(\bf{b-a}\right).\left(\bf{c-b}\right)&=0\\\Rightarrow\bf{b.c-b.b-a.c+a.b}&=0\\\Rightarrow\bf{b.c-b.b+a.b}=\bf{a.c}\end{align}$$ And we are looking for $\sqrt{\bf{x.x}}$, where $$\begin{split}\bf{x.x}&=\left(\bf{a+c-b}\right).\left(\bf{a+c-b}\right)\\&=\bf{a.a+b.b+c.c+}2\bf{a.c}-2\bf{a.b}-2\bf{c.b}\end{split}$$So, substituting $\bf{b.c-b.b+a.b}=\bf{a.c}$, $$\begin{split}\bf{x.x}&=\bf{a.a+b.b+c.c+}2\left(\bf{b.c-b.b+a.b}\right)-2\bf{a.b}-2\bf{c.b}\\&=\bf{a.a+b.b+c.c-}2\bf{b.b}\\&=\bf{a.a+c.c-b.b}\end{split}$$
But $\bf{a.a}$$=10^2=100,$ $\bf{b.b}$$=5^2=25,$ $\bf{c.c}$$=11^2=121$, so $\bf{x.x}$$=100+121-25=196=14^2$.
So the remaining distance is $14$.
