Diamond Ring
Find the radius of the stone in this ring.
Problem
Image
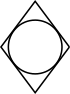
A circular stone is set in a rhombus so that it touches all four sides of the rhombus, as shown.
If the diagonals of the rhombus are 6 mm and 8 mm, what is the radius of the stone?
Student Solutions
The diagram below shows the diagonals:
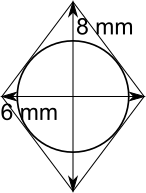
The diagonals of a rhombus cross at right angles, so four right-angled triangles are formed, as shown below (all lengths are in mm).
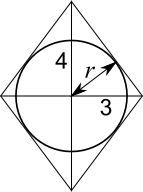
The hypotenuse of the right-angled triangle can be found using Pythagoras' Theorem. $$\begin{align}4^2+3^2&=c^2\\
\Rightarrow25&=c^2\\
\Rightarrow5&=c\end{align}$$
Just looking at that triangle, note that the radius meets the tangent at a right angle, so two smaller right-angled triangles are formed, as shown below.
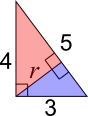
Each of the smaller right-angled triangles shares an angle with the larger right-angled triangle, so the three triangles are all similar. $r$ can be found using either triangle.
Consider the red triangle:
Its hypotenuse is $4$mm and the hypotenuse of the largest triangle is $5$mm, so the scale factor is $\frac{4}{5}$
$r$ is the shortest side of the red triangle, so $r=\frac{4}{5}\times 3 =2.4$ mm.
Consider the blue triangle:
Its hypotenuse is $3$mm and the hypotenuse of the largest triangle is $5$mm, so the scale factor is $\frac{3}{5}$
$r$ is the longer side of the blue triangle, so $r=\frac{3}{5}\times 4 = 2.4$ mm.
Alternatively, note that the area of the right-angled triangle is $3 \times 4=12\text{mm}^2$. We could also work out the area of the triangle by considering it to have a base of $5$ and a height of $r$, so $5r=12$ so $r=\frac{12}5=2.4$mm
Image

The diagonals of a rhombus cross at right angles, so four right-angled triangles are formed, as shown below (all lengths are in mm).
Image

The hypotenuse of the right-angled triangle can be found using Pythagoras' Theorem. $$\begin{align}4^2+3^2&=c^2\\
\Rightarrow25&=c^2\\
\Rightarrow5&=c\end{align}$$
Just looking at that triangle, note that the radius meets the tangent at a right angle, so two smaller right-angled triangles are formed, as shown below.
Image

Each of the smaller right-angled triangles shares an angle with the larger right-angled triangle, so the three triangles are all similar. $r$ can be found using either triangle.
Consider the red triangle:
Its hypotenuse is $4$mm and the hypotenuse of the largest triangle is $5$mm, so the scale factor is $\frac{4}{5}$
$r$ is the shortest side of the red triangle, so $r=\frac{4}{5}\times 3 =2.4$ mm.
Consider the blue triangle:
Its hypotenuse is $3$mm and the hypotenuse of the largest triangle is $5$mm, so the scale factor is $\frac{3}{5}$
$r$ is the longer side of the blue triangle, so $r=\frac{3}{5}\times 4 = 2.4$ mm.
Alternatively, note that the area of the right-angled triangle is $3 \times 4=12\text{mm}^2$. We could also work out the area of the triangle by considering it to have a base of $5$ and a height of $r$, so $5r=12$ so $r=\frac{12}5=2.4$mm
