Day Out

Answer: 35 km/h

Using a speed-time graph

Image

 

Image

 

Image

   

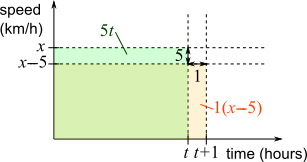
$\therefore 5t = x-5$ and $xt=210$

$5t = x-5\Rightarrow t = \frac{x-5}5$

$xt = 210 \Rightarrow x\left(\frac{x-5}5\right)=210\\

\hspace{18mm}\Rightarrow x(x-5)=1050\\

\hspace{18mm}\Rightarrow x^2-5x-1050=0$

The quadratic formula gives: $$\begin{align}x&=\frac{5\pm\sqrt{25--4200}}2\\

&=\frac{5\pm\sqrt{169\times25}}2\\

&=\frac{5\pm65}2\end{align}$$ So $x=35$

Using time = distance $\div$ speed

Average speed over $210$ km is $x$ km/h, then time is $\dfrac{210}x$ hours.

Planned average speed is $x-5$ km/h, time at planned speed $\dfrac{210}{x-5}$ hours.

$1$ hour earlier than planned, so $\dfrac{210}x$ is $1$ less than $\dfrac{210}{x-5}$, so $$\begin{align}&\frac{210}{x}=\frac{210}{x-5}-1\\ \hspace{1mm}\\

\Rightarrow&210=\frac{210x}{x-5}-x\\\hspace{1mm}\\

\Rightarrow&210(x-5)=210x-x(x-5)\\

\Rightarrow&210x-1050=210x-x^2+5x\\

\Rightarrow&x^2-5x-1050=0\\

\Rightarrow&(x+30)(x-35)=0\end{align}$$ So $x=-30$ or $x=35$. Since $x>0, x=35$.

Using distance = speed $\times$ time

If Chris completed the journey in $t$ hours, distance $=x\times t$.

Chris intended to take $t+1$ hours.

He intended to travel $5$ km/h slower, so at an average speed of $x-5$ km/h.

Distance $=(x-5)(t+1)=xt-5t+x-5$

Distances are the same so $xt = xt-5t+x-5\Rightarrow0=-5t+x-5\Rightarrow x=5t+5$

And $xt=210$ so $(5t+5)t=210\Rightarrow (t+1)t=42$ so $t, t+1$ could be $6,7$ (or $-6, -7$)

$x=5\times6+5=35$