Cubies
The scientists need your help to work out how many Cubies live on a small island! Use the cards to gather all the information you need.
Age
7 to 11
Challenge level
Problem
This problem has been designed to work on in a group of about four. For more details about how you might go about doing this, please read the Teachers' Resources.
Cubies are a race of tiny people who live on an island in the middle of the Indian Ocean. The island they live on is very small but their population is quite large. They live in a tall
building so they all have enough space to live on the island.
Scientists have been measuring the Cubies' population over the years but Cubies are very shy. When humans approach them they hide in their homes.
Over the years the scientists have recorded snippets of information in this table. This information will help you investigate the structure of the building and answer the following questions to help the scientists:
- How many flats are there on each floor of the building?
- How many Cubies are there in each family? For example, how many families are there with two Cubies in, perhaps a parent and a child Cubie? (We call these 'families of two'.) How many families of three Cubies are there? Can you keep going until you know exactly how many families of each size there are?
- Which families live on which floors? For example, how many families of two Cubies live on Floor A? What about Floor B? Can you keep going?
- What does the building itself look like? How are the flats arranged? Draw a diagram or make a model to show the scientists what you think!
With thanks to Jenny Piggott who created this task.
Image
Scientists have been measuring the Cubies' population over the years but Cubies are very shy. When humans approach them they hide in their homes.
Over the years the scientists have recorded snippets of information in this table. This information will help you investigate the structure of the building and answer the following questions to help the scientists:
- How many flats are there on each floor of the building?
- How many Cubies are there in each family? For example, how many families are there with two Cubies in, perhaps a parent and a child Cubie? (We call these 'families of two'.) How many families of three Cubies are there? Can you keep going until you know exactly how many families of each size there are?
- Which families live on which floors? For example, how many families of two Cubies live on Floor A? What about Floor B? Can you keep going?
- What does the building itself look like? How are the flats arranged? Draw a diagram or make a model to show the scientists what you think!
With thanks to Jenny Piggott who created this task.
Getting Started
How will you sort out all this information?
What do you need to know? How can you find this out/work this out?
Which clues have you already used? Which haven't you used yet? Are there any that aren't helpful?
Student Solutions
Elizabwe from Scotland sent in the following:
How many flats on each floor of the building: F 2, E 2, D 6, C 6, B 6, A2.
There are four families of 2, nine families of 3, twelve families of 4, two families of 5, one family of 6 and no families of seven.
Agatha, Charlie and Hector from Nutley CE Primary sent in the following:
Katey Daley, a Classroom Teacher from Kelvin Grove State College in Australia send in her class' work. Below you can see two parts and the full pdf can be viewed here.
Anthony from Tirlebrook Primary School sent in his work:
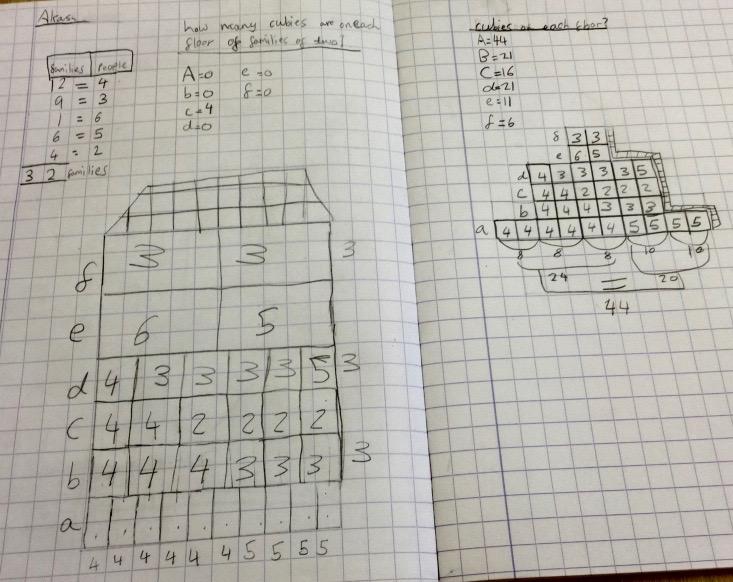
Akash from The British School of Brussels sent in an image of work done to solve this problem:
Phoebe from St Mary's Church of England Primary School Woodbridge wrote:
I found out the answers by reading the clues carefully to see which ones could be dismissed. Then I ticked the clues when I had used the information (to make it easier to see the remaining clues). I drew a picture to figure out the answers (using a pencil so I could rub out any mistakes). My proof is in the picture. This was easier than I thought when I got the hang of it.
Romilly also from St Mary's Church of England Primary School in Woodbridge wrote:
My answers are all shown in my picture. I worked out the answers by focusing on one question at a time. I read through the clues and crossed them out when I had used them. I worked out how many flats were on each floor first, then worked out how many families of each number there were. Then I could work out what the building looked like, it had to be symmetrical and the flats had to all be the same size (I used a ruler to make sure they were exactly the same size, and cubes!). Finally, I had to work out which family was where (I had to work out which floor they were on).
Frank and James Captain Elementary School in USA said:
First, we made a list of clues in a shorter format (eg. E = F # of flats). As we read the clues, we figured out that some of them were not connected to the problem we needed to solve. For example, “The bins are emptied on a Wednesday,” was not a clue that helped us figure out the number of flats, the shape of the building, the number of families or the number of cubies. This helped us eliminate clues that we didn't put in our list. After the first nine clues, we figured out how many flats were on each floor and we used wooden cubes to build a model of the block. We then drew a picture of it in our notebooks.
Once we got through 11 clues, we realized that a chart would help us keep track of the size and number of Cubie families better. Down the side, we had the names of each of the floors. Across the top, we had the possible number of cubies per family. We made a second part of the chart below the first that tracked the number of families in the block that have each different number of cubies. On the chart, we started with checks and xs to represent whether there were families of that size on that floor. As we got new clues, we replaced the checks with the number of families that size on that floor.
Finally, once we had gathered all the clues and put them in our chart, then we multiplied the number of cubies per family by the number of families that size on that floor (eg. 6 families of 4 (24) AND 4 families of 5 (20) live on Floor A, so there are 44 cubies on floor A ). After multiplying we added all the cubies on each floor to find a total population. We found that 119 cubies live in the block.
Thank you for these solutions, particularly those that have given detail about how you went about the task.
How many flats on each floor of the building: F 2, E 2, D 6, C 6, B 6, A2.
There are four families of 2, nine families of 3, twelve families of 4, two families of 5, one family of 6 and no families of seven.
Agatha, Charlie and Hector from Nutley CE Primary sent in the following:
Image
Katey Daley, a Classroom Teacher from Kelvin Grove State College in Australia send in her class' work. Below you can see two parts and the full pdf can be viewed here.
Image
Image
Anthony from Tirlebrook Primary School sent in his work:
Image
Akash from The British School of Brussels sent in an image of work done to solve this problem:
Image
Phoebe from St Mary's Church of England Primary School Woodbridge wrote:
I found out the answers by reading the clues carefully to see which ones could be dismissed. Then I ticked the clues when I had used the information (to make it easier to see the remaining clues). I drew a picture to figure out the answers (using a pencil so I could rub out any mistakes). My proof is in the picture. This was easier than I thought when I got the hang of it.
Image
Romilly also from St Mary's Church of England Primary School in Woodbridge wrote:
My answers are all shown in my picture. I worked out the answers by focusing on one question at a time. I read through the clues and crossed them out when I had used them. I worked out how many flats were on each floor first, then worked out how many families of each number there were. Then I could work out what the building looked like, it had to be symmetrical and the flats had to all be the same size (I used a ruler to make sure they were exactly the same size, and cubes!). Finally, I had to work out which family was where (I had to work out which floor they were on).
Image
Frank and James Captain Elementary School in USA said:
First, we made a list of clues in a shorter format (eg. E = F # of flats). As we read the clues, we figured out that some of them were not connected to the problem we needed to solve. For example, “The bins are emptied on a Wednesday,” was not a clue that helped us figure out the number of flats, the shape of the building, the number of families or the number of cubies. This helped us eliminate clues that we didn't put in our list. After the first nine clues, we figured out how many flats were on each floor and we used wooden cubes to build a model of the block. We then drew a picture of it in our notebooks.
Once we got through 11 clues, we realized that a chart would help us keep track of the size and number of Cubie families better. Down the side, we had the names of each of the floors. Across the top, we had the possible number of cubies per family. We made a second part of the chart below the first that tracked the number of families in the block that have each different number of cubies. On the chart, we started with checks and xs to represent whether there were families of that size on that floor. As we got new clues, we replaced the checks with the number of families that size on that floor.
Finally, once we had gathered all the clues and put them in our chart, then we multiplied the number of cubies per family by the number of families that size on that floor (eg. 6 families of 4 (24) AND 4 families of 5 (20) live on Floor A, so there are 44 cubies on floor A ). After multiplying we added all the cubies on each floor to find a total population. We found that 119 cubies live in the block.
Thank you for these solutions, particularly those that have given detail about how you went about the task.
Teachers' Resources
Cubies
This problem has been designed to work on in a group of about four. For more details about how you might go about doing this, please read the Teachers' Resources.Image
Scientists have been measuring the Cubies' population over the years but Cubies are very shy. When humans approach them they hide in their homes.
Over the years the scientists have recorded snippets of information in this table. This information will help you investigate the structure of the building and answer the following questions to help the scientists:
- How many flats are there on each floor of the building?
- How many Cubies are there in each family? For example, how many families are there with two Cubies in, perhaps a parent and a child Cubie? (We call these 'families of two'.) How many families of three Cubies are there? Can you keep going until you know exactly how many families of each size there are?
- Which families live on which floors? For example, how many families of two Cubies live on Floor A? What about Floor B? Can you keep going?
- What does the building itself look like? How are the flats arranged? Draw a diagram or make a model to show the scientists what you think!
With thanks to Jenny Piggott who created this task.
Why do this problem?
This problem will encourage learners to organise information, identify redundant information and to check their work.
The activity lends itself to collaborative working, both for children who are inexperienced at working in a group and children who are used to working in this way. By working together on this problem, the task is shared and therefore becomes more manageable than if working alone.
Many NRICH tasks have been designed with group work in mind. Here we have gathered together a collection of short articles that outline the merits of collaborative work, together with examples of teachers' classroom practice.
Many NRICH tasks have been designed with group work in mind. Here we have gathered together a collection of short articles that outline the merits of collaborative work, together with examples of teachers' classroom practice.
Possible approach
This is an ideal problem for learners to tackle in groups of four. Allocating these clear roles (word, pdf) can help the group to work in a purposeful way - success on this task could be measured by how effectively the group works together as well as by the letters they compose. This version of the roles has been adapted for primary children.Introduce the four group roles to the class. It may be appropriate, if this is the first time the class has worked in this way, to allocate particular roles to particular children. If the class works in roles over a series of lessons, it is desirable to make sure everyone experiences each role over time.
For suggestions of team-building maths tasks for use with classes unfamiliar with group work, take a look at this article and the accompanying resources.
As a class, read through the description of the task. Each group of four will need a copy of these cards (word, pdf) which should be shared between all members of the group. Ask the children to read through the cards. Explain that the groups will feed back at the end of the session, sharing the ways they worked, what helped them and what got in the way. You could give each group a large sheet of flipchart paper on which to draw the block and write their thoughts about the way they worked etc. in preparation for the feedback.
While groups are working, label each table with a number or letter on a post-it note, and divide the board up with the groups as headings. Listen in on what groups are saying, and use the board to jot down comments and feedback to the children about the way they are working together.
You may choose to focus on the way learners are co-operating, for example:
Group A - Good to see you listening carefully to each other.
Group B - Facilitator - is everyone in your group contributing?
Group C - I like the way you are sorting the cards together.
Alternatively, your focus for feedback might be mathematical, for example:
Group A - I like the method you're using to record which Cubies live on which floor.
Group B - How do you know that there are six flats on Floor C?
Make sure that while groups are working they are reminded of the need to be ready to present their work at the end, and that all are aware of how long they have left.
It might be best to display each group's poster and let everyone look at the other groups' work. You could then ask a few groups to explain their solution and to give more detail about the way they worked, leaving time for questions from the rest of the class.
Key questions
If your focus is effective group work, this list of skills may be helpful (word, pdf). Ask learners to identify which skills they demonstrated, and which skills they need to develop further.If your focus is mathematical, these prompts might be useful:
How will you sort out all this information?
What do you need to know? How can you find this out/work this out?