Crossover
The numbers 2 to 8 are to be placed in the diagram so that the row and column each adds to 21. Which numbers can replace x?
Age
11 to 14
Challenge level
Problem
Image
The numbers $2$, $3$, $4$, $5$, $6$, $7$ and $8$ are placed in the squares in this diagram.
The four numbers in the horizontal row add up to $21$, and the four numbers in the vertical column also add up to $21$.
Which number should replace $x$?
If you liked this problem, here is an NRICH task that challenges you to use similar mathematical ideas.
Student Solutions
Answer: 7
Using totals
Image
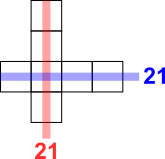
21 + 21 = 42
2 + 3 + 4 + 5 + 6 + 7 + 8 = 35
7 missing so the 7 is couted twice
x = 7
Using totals and symbols
Image
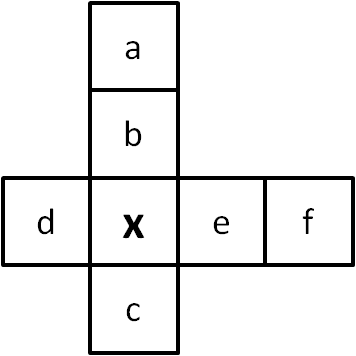
$a+b+x+c = 21$
$d+x+e+f = 21$
$d+x+e+f = 21$
Then, the letters $a$, $b$, $c$, $d$, $e$, $f$ and $x$ are, in some order, $2$, $3$, $4$, $5$, $6$, $7$ and $8$. This means that their sums must be the same, so;$$a+b+c+d+e+f+x = 2+3+4+5+6+7+8 = 35.$$ Then, if the equations at the top are added together, these give:$$a+b+c+d+e+f+2x=42.$$
Image
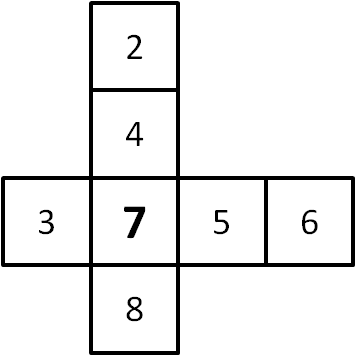
This value of $x$ can be achieved as shown in the diagram on the right.