Crane arm
A parallelogram is formed by joining together four equilateral triangles. What is the length of the longest diagonal?
Age
14 to 16
Challenge level
Problem
Image
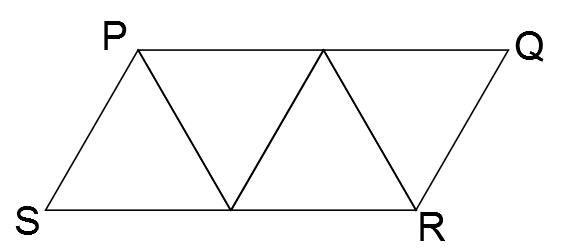
The parallelogram PQRS is formed by joining together four equilateral triangles of side 2 units, as shown.
What is the length of the diagonal SQ?
If you liked this problem, here is an NRICH task that challenges you to use similar mathematical ideas.
Student Solutions
Image
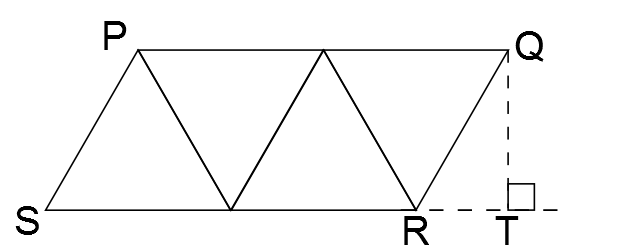
In the diagram, T is the foot of the perpendicular from Q to the extension of SR. All of the angles in the equilateral triangles are 60 °, so ∠QRT is also 60 °. Then ΔQRT is a right-angled triangle, so we can show that the lengths of RT and QT are $1$ and $\sqrt{3}$ respectively.
Applying Pythagoras' Theorem to ΔQST, $SQ^2 = ST^2 + QT^2 = 5^2 + (\sqrt{3})^2 = 28$.
So the length of SQ is $\sqrt{28}=2\sqrt{7}$ units.