Converging quadrilaterals
Explore the properties of this iterative geometrical procedure
Problem
Note that this open investigation can be taken to many levels of complexity.
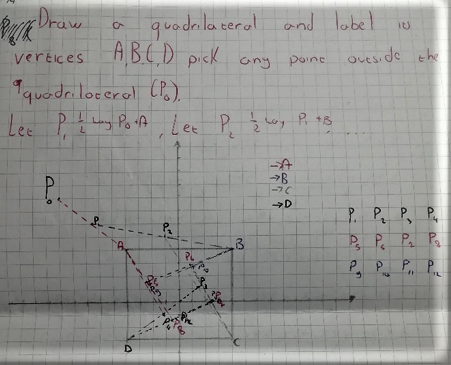
Draw a quadrilateral and label its vertices $A, B, C$ and $D$. Pick any point $P_0$ outside the quadrilateral. Apply the following operations to generate eight new points:
- Let $P_1$ be the point half way between $P_0$ and $A$
- Let $P_2$ be the point half way between $P_1$ and $B$
- Let $P_3$ be the point half way between $P_2$ and $C$
- Let $P_4$ be the point half way between $P_3$ and $D$
- Let $P_5$ be the point half way between $P_4$ and $A$
- Let $P_6$ be the point half way between $P_5$ and $B$
- Let $P_7$ be the point half way between $P_6$ and $C$
- Let $P_8$ be the point half way between $P_7$ and $D$
Explore the properties of this sequence and its continuation. You might like to use geogebra or other tools alongside a pen and paper analysis.
For more investigations see our Stage 5 pages.
Student Solutions
Radif from the London Academy of Excellence Tottenham in the UK sent in this solution:
First I drew the graph on a piece of paper, using a regular quadrilateral just to make the thing simple. I noticed that as you continue to plot the points following the sequence, the points start to lie more or less on the same position.
Thinking about how this was possible I tackled this question algebraically:
Let $P_0$ be $(X, Y)$
Let $A$ be $(X_1, Y_1)$
Let $B$ be $(X_2, Y_2)$
Let $C$ be $(X_3, Y_3)$
Let $D$ be $(X_4, Y_4)$
Then I started to express the $P$'s points in terms of $P_0, A, B, C$ and $D$; getting [a] long algebraic expression. Every 4 points the [pattern] started again so the point $P_4$ would lie near $P_8, P_{12}, P_{16}...$.
Click to see Radif's work up to $P_8$

Click to see Radif's work from $P_9$ to $P_{12}$

Click to see the pattern Radif found between the terms
I noticed a strange coincidence with the coefficient[s] [of $x_1, x_2, x_3$ and $x_4$] as they seem to increase in a specific pattern.
In maths, it is not usually a coincidence, it happens for a reason - why does this pattern emerge?

(Note that Radif has stopped giving the $y$ coordinates and is now using $P_a$ to denote the $x$ coordinate only)
I then found some interesting ratios,
- The coefficient[s] of [$x_1, x_2, x_3$ and $x_4$ in] every fourth point [are] $n\times2^0,$ $n\times2^1,$ $n\times2^2,$ $n\times2^3$ [respectively]
- [For the point $P_k$,] the denominator is always $2^{k}$ (which was predictable)
- The $\frac{(\text{Denominator}-1)}{\text{the coefficient }n}$ is ALWAYS $15$
This allows us to predict any future points after $P_{16}$ (which is the point I went up to) (fourth points only, where $a$ is a multiple of $4$)
So $P_a=\dfrac{x + \left(\left(2^a-1\right)\div15\right) \times 2^\text{[0 for the first and then 1,2 and 3]}}{2^a}$
Radif means: when $a$ is a multiple of $4$, the $x$-coordinate of $P_{a}$ will be $\dfrac{x + \left(\left(2^{a}-1\right)\div15\right)\left(2^0x_1+2^1x_2+2^2x_3+2^3x_4\right)}{2^a}$
This may explain the reason why every 4th point lies on similar points: as the numerator increases the denominator also increases by a similar amount, therefore the ratio will be similar if not equal.
It seemed finished, but then I asked myself, is this always true for every shape? I then tried the same thing on [a] triangle.
Click to see Radif's work for a triangle
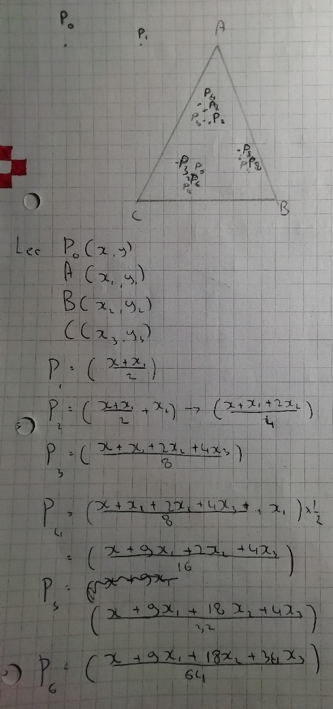

And then unsurprisingly the same thing happened so
The coefficient of [$x_1, x_2, x_3$] every fourth (this should be third) point is $n\times2^{[0, 1 or 2]}$ and the $\dfrac{\text{Denominator-1}}{\text{the coefficient }n}$ is this time $7.$
So Radif means that every third point, ie. $P_a$ where $a$ is a multiple of $3$ has $x$-coordinate $\dfrac{x + \left(\left(2^a-1\right)\div7\right)\left(2^0x_1+2^1x_2+2^2x_3\right)}{2^a}$
And again I then tried using a different shape, this time a pentagon.
Click to see Radif's work for a pentagon.


The exact same thing happened so the coefficient of P every four (Radif means fifth) point is $n\times2^ {[0, 1, 2, 3 \text{ or }4]}$ AND $\dfrac{\text{Denominator-1}}{\text{the coefficient }n}$ is this time $31.$
So Radif means that every fifth point, ie. $P_a$ where $a$ is a multiple of $5$ has $x$-coordinate $\dfrac{x + \left(\left(2^a-1\right)\div31\right)\left(2^0x_1+2^1x_2+2^2x_3+2^3x_4+2^4x_5\right)}{2^a}$
Click to see Radif's conclusions about all shapes.
After some calculation I then found out where the number 7,15 and 31 came from.
The power of $2^{\text{# of sides}} - 1$ gives you the constant for the equations so from here I deduced a kind of "universal equation" for every kind of shape, which is ...
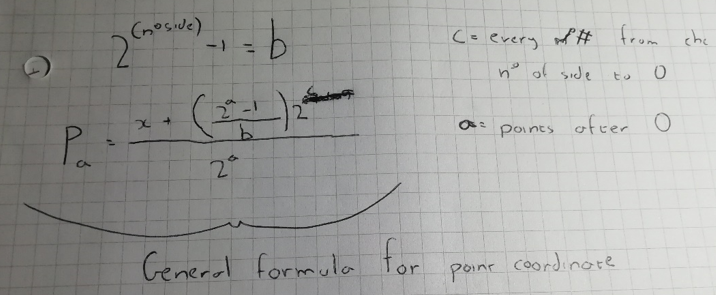
What Radif means is, that, for a shape with $s$ sides, the pattern will repeat every $s$ points. When $a$ is a multiple of $s$, the $x$-coordinate of $P_a$ will be: $\dfrac{x + \left(\left(2^a-1\right)\div(2^s-1)\right)\left(2^0x_1+2^1x_2+ ... +2^{s-1}x_s\right)}{2^a}$
