Comparing totals

Answer: 14

Balancing numbers at each end

Adding from 1 will be the same as adding from 20

Use up the large numbers by balancing them with little numbers

$20=4\times5$ so use $4$ numbers close to $5$ to make $20$:

Image

 

$19=9+10$

Image

 

$18=5+2+11$

Image

There aren't enough small numbers to make $17$ so take $16$ and $17$ together $=33$

Use up the $8:\ \ \ 33-8=25=12+13$

Image

 

Which leaves $14+1=15$

Image

 

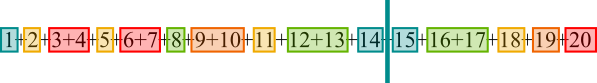
So the sum from $1$ to $14$ is the same as the sum from $15$ to $20$.

Adding up all of the numbers

Image

 

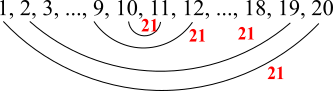
10 pairs of numbers which add up to 21

$\therefore$ sum of all 20 = 10$\times$21 = 210

Each sum is equal to 210$\div$2 = 105

Add up until 105 - quicker using larger numbers

20 + 20 + 20 + 20 + 20 = 5 less than 105

20 + 19 + 18 + 17 + 16 = 5 + 1 + 2 + 3 + 4 less than 105 = 15 less than 105

20 + 19 +          ...         + 15 = 105

$n$ is 14

Comparing Milly's sum to $1+2+3+4+...+20$

Milly's and Billy's sums are equal and add up to $1+2+3+4+...+20$, so Milly's sum must be equal to half of $1+2+3+4+...+20.$

So $$\begin{split}1+2+3+4+...+n&=\dfrac{1+2+3+4+...+20}{2}\\&=\tfrac{1}{2}+\tfrac{2}{2}+\tfrac{3}{2}+\tfrac{4}{2}+...+\tfrac{20}{2}\\

&=\tfrac{1}{2}+1+1\tfrac{1}{2}+2+...+10\end{split}$$

Rewriting the right hand side to put the integers first, we can begin to subtract numbers from both sides:

$$\begin{align}1+2+3+4+...+10+&11+...+n=1+2+3+...+10+\tfrac{1}{2}+1\tfrac{1}{2}+2\tfrac{1}{2}+...+9\tfrac{1}{2}\\\Rightarrow &11+...+n=\tfrac{1}{2}+1\tfrac{1}{2}+...+9\tfrac{1}{2}\end{align}$$

Now, looking at the right hand side, $1\frac{1}{2}+9\frac{1}{2}=11$, so we can remove 11 from both sides of the equation:

$$12+...+n=\frac{1}{2}+2\frac{1}{2}+3\frac{1}{2}+4\frac{1}{2}+5\frac{1}{2}+6\frac{1}{2}+7\frac{1}{2}+8\frac{1}{2}$$.

Similarly, $3\frac{1}{2}+8\frac{1}{2}=12$ and $5\frac{1}{2}+7\frac{1}{2}=13$.

Removing those from the left and right hand side just leaves

$\frac{1}{2}+2\frac{1}{2}+4\frac{1}{2}+6\frac{1}{2}$ on the right hand side, which is equal to $14,$

so $n=14.$

Using formulae

Using the formula that $1+2+3+...+r=\frac{1}{2}r(r+1)$ for any whole number $r$, Milly's sum is equal to $\frac{1}{2}n(n+1)$ and $1+2+3+...+20=\frac{1}{2}20(21)=210.$

Since Milly's and Billy's sums are equal and add up to $210$, Milly's sum must be equal to half of $210,$ so $\frac{1}{2}n(n+1)=105

\Rightarrow n(n+1)=210.$

From here, you could find $n$ using factorisation ($210=2\times3\times5\times7=14\times15$), or expand and solve the quadratic equation $n^2+n-210=0$

By factorisation

$(n-14)(n-15)=0\Rightarrow n=14$ or $n=-15,$ so $n=14$ since $n$ is positive.

Using the quadratic formula

Let $a=1,$ $b=1,$ $c=-210$ and $n=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$ $$\begin{align}n&=\dfrac{-1\pm\sqrt{1--4\times1\times210}}{2}\\&=\dfrac{-1\pm\sqrt{841}}{2}\\&\dfrac{-1\pm29}{2}\end{align}$$ Which gives $

n=14$ or $n=-15,$ so $n=14$ since $n$ is positive.