Circled square
Can you find the area of this square inside a circle?
Age
14 to 16
Challenge level
Problem
Image
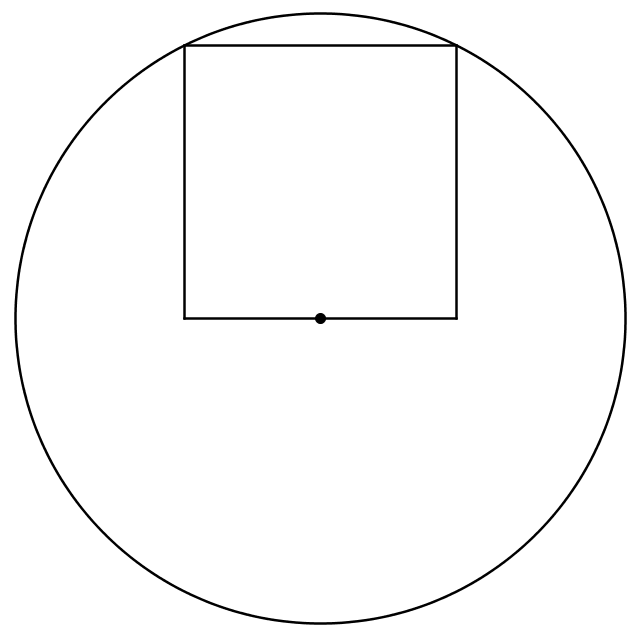
The circle has radius 1 cm.
Two vertices of the square lie on the circle.
One edge of the square goes through the centre of the circle, as shown.
What is the area of the square?
This problem is taken from the UKMT Mathematical Challenges.
One edge of the square goes through the centre of the circle, as shown.
What is the area of the square?
This problem is taken from the UKMT Mathematical Challenges.
Student Solutions
Image
Suppose the side length is $s$ cm, then the area is $s^2$ cm$^2$.
The radius of the circle is 1 cm, so the distance from the centre of the circle ($O$) to the vertices of the square that touch the circumference ($Q$ and $R$) is 1 cm.
This, the side length $s$ and the half-side length $\frac{1}{2}s$ are shown on the diagram:
Angle $OSR$ is a right angle (as it is in a square), so applying Pythagoras' theorem to triangle $OSR$ gives
$$\begin{align} s^2+(\frac{1}{2}s)^2 &= 1^2 \\
\Rightarrow s^2+\frac{1}{4}s^2 &= 1\\
\Rightarrow \frac{5}{4}s^2 &= 1\\
\Rightarrow s^2&=\frac{4}{5}\end{align}$$So the area of the square is $\dfrac{4}{5}$cm$^2$.