Circle time
Three circles of different radii each touch the other two. What can you deduce about the arc length between these points?
Age
14 to 16
Challenge level
Problem
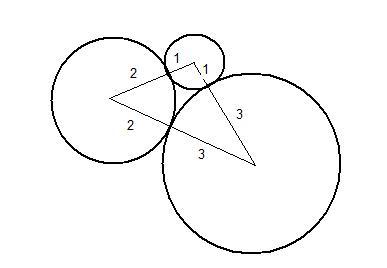
Three circles $C_1$, $C_2$ and $C_3$, of radii 1 cm, 2 cm and 3 cm respectively touch as shown. $C_1$ meets $C_2$ at $P$ and meets $C_3$ at $Q$.
Image
What is the length in cm of the longer arc of circle $C_1$ between $P$ and $Q$?
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Student Solutions
The triangle that joins up the centres of the circles has sides of length 3 cm, 4 cm, 5 cm so must be a right angled triangle by the converse of Pythagoras' Theorem. Therefore the length of the longer arc of the circle $C_1$ is $\frac{3}{4} \times 2\pi \times 1 = \frac{3}{2} \pi$ cm.
Image
