Christmas Chocolates
How could Penny, Tom and Matthew work out how many chocolates there are in different sized boxes?
Problem
Penny, Tom and Matthew were each given mint chocolates in a hexagonal box:
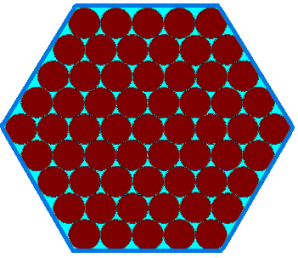
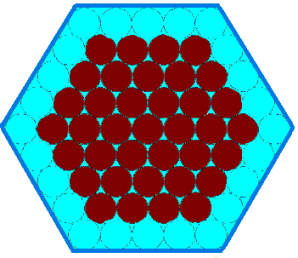
Penny, Tom and Matthew have been promised a larger box of chocolates as a Christmas present from their grandmother. The box will have $10$ chocolates along each edge, instead of just $5$.
How would each child work out how many chocolates the larger box will contain?
Can you describe any other ways to work it out?
Here are some more questions you might like to consider:
- For which sizes of chocolate box will the three children be able to share the chocolates equally?
- For which sizes of chocolate box will the boys be able to share the chocolates equally?
- Can you describe how each child would work out the number of chocolates in a box with $n$ chocolates along each edge?
Getting Started
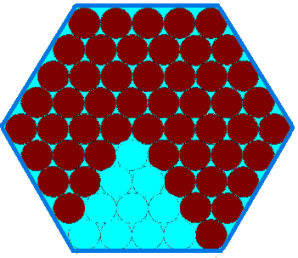
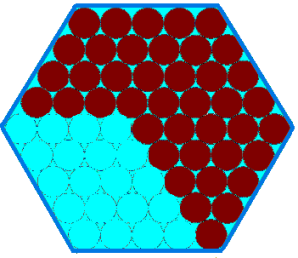
Which $10$ chocolates do you think Penny will eat next?
Which $20$ chocolates do you think Tom will eat next?
Student Solutions
This problem demonstrates that multiple, different methods can be used to approach a particular question. In addition, you are encouraged to devise a general formula for the number of chocolates in any hexagonal box. In doing this, it then becomes very straightforward to work out the number of chocolates there are, however large the box is.
Working out general formulae is not only fun and satisfying, but is also very useful; it provides a quick way to extend the original set of data, without having to work out every consecutive point. Scientists, Mathematicians, Engineers, Accountants...they all find general formulae very helpful, and make use of them regularly.
In the Christmas Chocolates problem, the formula can be extended to any size of box, because the differences are uniformly spaced. However, sometimes we do not have "perfect" information. For example, an experiment may yield slightly different results each time (this is why we do repeat experiments), but we cannot do an infinite number of trials. Thus we settle on an appropriate number, and then use the data collected to see if there is a pattern. From this, perhaps with more experiments, we may be able to devise a general formula. This can then be used to make predictions, and then experiments can be used to test these. The formula may then be refined, and then new predictions made, and so on. Remember though that the formula may not be true for all conditions, unlike the chocolate problem. For example, the formula may only apply within a given temperature range. Nevertheless, having a formula is very useful; it not only makes calculations more efficient, but can also yield great insight into the properties of the problem.
Lots of great solutions were submitted, so thank you to everyone for this! Many students noticed the shapes that were made once Penny, Tom, and Matthew had eaten some chocolates. They then realised that several of these shapes could fit into the whole hexagonal box. This is useful as it provides a convenient way of grouping the chocolates together, and therefore quickens calculations. The patterns can then be used to extend to other box sizes, as several students did.
Courtney, from Penrhos College, submitted this solution. It is lovely: clear, and illustrated. Lauren, from Tudhoe Grange, also submitted a good solution. This solution is colourful, and demonstrates the different shapes created by Penny, Tom, and Matthew very clearly. Adam, from Wilson's School explained:
Another way to work it out would be to add the rows up.
Luke, from Wilmslow High School, used the alternative method suggested by Adam. In his solution, he added the rows of the hexagon up to find out the total number of chocolates in the box.
Monty, from The Perse School, and Claudia & Martha from Impington Village College noticed that Penny and Tom's methods were extremely similar; Tom ate twice as much as Penny, so the only difference between the caluclation is a factor of two!
Philip, from Wilson's School extended the methods used by Penny, Tom, and Matthew to work out the number of chocolates in a box with ten along each edge:
You can begin to see a pattern; the hexagonal box can always be divided into six triangles, or three parallelograms, or can be stripped down layer by layer like Matthew did. This is true whatever size the box is (as long as it has six sides). This important characteristic can then be used as a starting point for developing a general formula for the number of chocolates in the box. Philip from Gosforth High School used the pattern:
Kevin, Leif, Oliver, Nisha, Olivia, Thomas, and Henry from Highgate School explained the latter point made by Hannah and Phil (about sharing the chocolates equally). They used Matthew's method as an example:
They then applied the same principle to work out the size of chocolate box the boys will be able to share out equally (i.e. between two people):
In fact, as Philip from Wilson's School pointed out:
What's the moral of this, then? Well, if you want to share a box of chocolates equally between two or three people, it should not be a hexagonal box like the one in the question. You could, of course, not share it equally... and have more for yourself... Even better, give more to somebody else!
Thank you to everyone who submitted solutions to this tasty chocolatey problem. If you enjoyed this (and we know that you did!), have a go at Summing Squares and Picture Story. These problems are nice extensions of this chocolate problem. If you would like to try a similar, related problem for more practice, try Picturing Triangle Numbers, Mystic Rose, or Handshakes.
Teachers' Resources
Why do this problem?
Many students are accustomed to using number patterns in order to generalise. This problem offers an alternative approach, challenging students to consider multiple ways of looking at the structure of the problem. The powerful insights from these multiple approaches can help us to derive general formulae, and can lead to students' appreciation of the equivalence of different algebraic expressions.
Possible approach
Challenge students to express each method for finding the number of chocolates in any size of box, perhaps introducing some algebra and the idea of a size $n$ box if appropriate.
Bring the class together to share findings. Compare the different "formulae" which have emerged, and ask students to explain why they are equivalent.
Key questions
Possible extension
The problems Summing Squares and Picture Story lead to formulae for some intriguing sequences through analysis of the structure of the contexts.
Possible support
The problem Seven Squares gives lots of simple contexts where formulae emerge by looking at structure rather than number sequences.
