Chippy's journeys
Chippy the Robot goes on journeys. How far and in what direction
must he travel to get back to his base?
Age
7 to 11
Challenge level
Problem
Chippy the Robot was sent on a journey.
Image
Chippy started from his base station and went $2$m (metres) N (North).
Then he turned and went $2$m E (East), $3$m N, then $3$m W (West) and $2$m S (South).
After that he went $2$m E, $3$m N and $3$m W again.
Then he went $5$m S and $4$m E.
Finally, he went $1$m S.
There he stopped.
How many metres altogether did Chippy travel on that journey?
How far and in what direction must Chippy travel to get back to his base station?
The next day Chippy went on another journey.
This time he started $3$ m (metres) West and $4$ m North of his base station. He went $6$ m E, $2$ m N, $4$ m W and $1$ m S. He then turned round and retraced his movements for $4$ m.
Where did he end up?
Can you find the shortest route to get him back to his base station?
How many metres did he have to go to get back?
Can you find him a route back which is exactly $12$ m?
How many different $12$ m routes can you find?
Getting Started
How about using squared paper to draw out Chippy's routes?
What will $1$ square on the paper stand for in metres?
Student Solutions
We received lots of correct answers to the first part of this problem but very few of you told us how you went about solving it. Some of you drew a diagram of Chippy's route, which was a very good way of tackling it. Rukmini from Hopscotch Nursery and Christy, sent particularly clear pictures. Here is Rukmini's:
Image
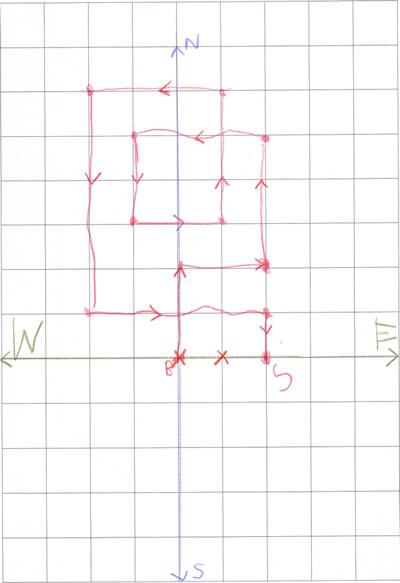
Rukmini says:
First I took some checked paper and drew a map showing North,
East, West and South. In the centre was the Base station which I
marked as B on the map. From B, I counted squares Chippy went
along. He seemed to go a bit round and round till he forgot where
the basic station was. I marked with a 'S' where he stopped. I drew
his way back with crosses. He needed to go $2$ m West to get back
to the Base station.
Tom who lives in New Zealand, solved the the first part of problem in a different, but equally as good way. Here is what Tom says:
This is a table showing how many metres Chippy went:
| N | S | E | W | |
| 2 | 2 | 2 | 3 | |
| 3 | 5 | 2 | 3 | |
| 3 | 1 | 4 | ||
| Total | 8 | 8 | 8 | 6 |
The north and the south amounts were the same so there was no
change there, but the east and the west amounts were different. The
east was $2$ metres more than the west. So you have to go $2$
metres in west at the end to get to Chippy's station.
Well done to you all for your well explained solutions.
Teachers' Resources
Chippy's Journeys
Chippy the Robot was sent on a journey.
Image
Chippy started from his base station and went $2$m (metres) N (North).
Then he turned and went $2$m E (East), $3$m N, then $3$m W (West) and $2$m S (South).
After that he went $2$m E, $3$m N and $3$m W again.
Then he went $5$m S and $4$m E.
Finally, he went $1$m S.
There he stopped.
How many metres altogether did Chippy travel on that journey?
How far and in what direction must Chippy travel to get back to his base station?
The next day Chippy went on another journey.
This time he started $3$ m (metres) West and $4$ m North of his base station. He went $6$ m E, $2$ m N, $4$ m W and $1$ m S. He then turned round and retraced his movements for $4$ m.
Where did he end up?
Can you find the shortest route to get him back to his base station?
How many metres did he have to go to get back?
Can you find him a route back which is exactly $12$ m?
How many different $12$ m routes can you find?
Why do this problem?
This problem will help to reinforce compass directions and to develop familiarity with measurement in metres.
It is an ideal opportunity for learners to use and record the vocabulary of position and direction. It could be a good time to introduce the four compass directions to describe movement about a grid.
When the problem is done on squared paper it is also an excellent opportunity to introduce the idea of scale in its most basic form.
Possible approach
If space allows, you could start by tackling this problem practically with the class working outside or in the hall using a grid drawn on the ground. An $8$ by $8$ grid is required.
Alternatively, you could start using squared paper. This is, in any case, the next stage. You could use this image of the required grid on an interactive white board or simply draw an $8$ by $8$ grid.
After this learners could work in pairs on the actual problem from a computer or this printed sheet so that they are able to talk through their ideas with a partner. (The sheet has the whole problem, without the picture, but with a small grid which could be copied onto
squared paper.) Two larger copies of the grid can be found here.
At the end of the lesson, besides the solutions, the discussion could include reinforcement of any vocabulary used or introduced, and of how the four compass directions can describe the movement about a grid.
Key questions
How about using squared paper to draw out Chippy's route?
What will one square on the paper stand for in metres?
In which direction is North/South/East/West?
Why don't you draw the compass points on your grid?
How far does Chippy go in that direction? So where does he end up?