A Cartesian puzzle
Find the missing coordinates which will form these eight quadrilaterals. These coordinates themselves will then form a shape with rotational and line symmetry.
Problem
Here are the coordinates of some quadrilaterals, but in each case one coordinate is missing! The coordinates are given going round each quadrilateral in an anti-clockwise direction.
- $(2,11), \; (0,9),\; (2,7),\; (?,?)$
- $(3,7),\; (3,4),\; (8,4),\; (?,?)$
- $(18,3),\; (16,5), \;(12,5),\; (?,?)$
- $(13,12),\; (15,14),\; (12,17),\; (?,?)$
- $(7,14),\; (6,11),\; (7,8),\; (?,?)$
- $(15,9),\; (19,9),\; (16,11),\; (?,?)$
- $(11,3),\; (15,2),\; (16,6),\; (?,?)$
- $(9,16),\; (2,9),\; (9,2),\; (?,?)$
The quadrilaterals are all symmetrical. They may have rotational symmetry, or line symmetry, or both.
Can you work out what the missing coordinates are if you know they are all positive? Is there more than one way to find out?
Now plot those eight missing coordinates on a graph like the one below.
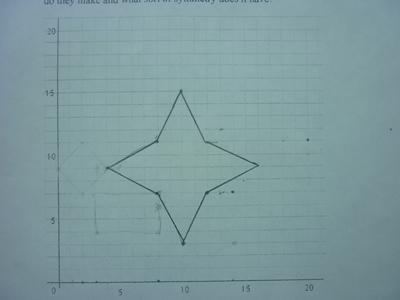
What shape do they make and what sort of symmetry does it have?
Getting Started
The shapes include one parallelogram, on trapezium and one rhombus, and are otherwise squares and rectangles.
Student Solutions
We have had the following solution from Matthew, David and Jack at St. Nicolas School, Newbury. They thought there was a problem with number 6 but there isn't!
Our solutions to the missing coordinates are:
- (2,11), (0,9), (2,7) ..............(4,9)
which had both rotational and line symmetry. - (3,7), (3,4), (8,4) ..............(8,7)
which had both rotational and line symmetry. - (18,3), (16,5), (12,5) ..............(10,3)
which had line symmetry. - (13,12), (15,14), (12,17) ..............(10,15)
which had both rotational and line symmetry. - (7,14), (6,11), (7,8) ..............(8,11)
which had both rotational and line symmetry. - (15,9), (19,9), (16,11) ..............(12,11)
which had rotational symmetry. - (11,3), (15,2), (16,6) ..............(12,7)
which had both rotational and line symmetry. - (9,16), (2,9), (9,2) ..............(16,9)
which had both rotational and line symmetry.
We plotted these 8 sets of coordinates, which made a symmetrical star.
We also heard from George and Thalia from Hoyle Court Primary School, Baildon who worked together to complete the puzzle. Their teacher wrote:
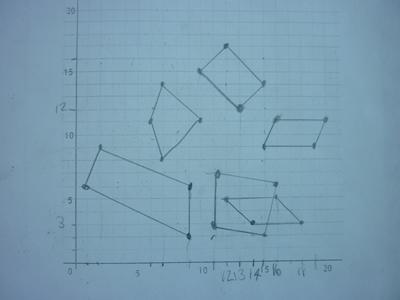
They worked out the missing co-ordinates for the quadrilaterals then tried to produce the final symmetrical shape.
At first their shape was not symmetrical. They realised it should be a star and corrected the two inaccurate co-ordinates.
Then went back and drew the original two quadrilaterals again using the amended co-ordinates from the star.
Great teamwork!!
Here are photos of their symmetrical star and some of their initial quadrilaterals:
The students in 5D at Vienna International School have been working on this.
They think they have come up with a way to find the missing coordinate without using the grid.
Let's take the first example: (2,11), (0,9), (2,7)
Take the first and third x axis coordinate and add them together. Subtract the second x axis coordinate. This give you 4.
Take the first and third y axis coordinate and add them together. Subtract the second y axis coordinate. This give you 9..
Their process seems to work for all of the examples here. They drew their own symmetrical quadrilaterals and gave three coordinates in an anticlockwise direction to a friend. Using the same process their friends tried to work out the fourth coordinate. It worked in each case.
Well done to Chrysanthi, Kathy, Jack, Samuel, Erik, Timothy for their persistence with this.
Teachers' Resources
A Cartesian Puzzle
Here are the coordinates of some quadrilaterals, but in each case one coordinate is missing! The coordinates are given going round each quadrilateral in an anti-clockwise direction.
- $(2,11), \; (0,9),\; (2,7),\; (?,?)$
- $(3,7),\; (3,4),\; (8,4),\; (?,?)$
- $(18,3),\; (16,5), \;(12,5),\; (?,?)$
- $(13,12),\; (15,14),\; (12,17),\; (?,?)$
- $(7,14),\; (6,11),\; (7,8),\; (?,?)$
- $(15,9),\; (19,9),\; (16,11),\; (?,?)$
- $(11,3),\; (15,2),\; (16,6),\; (?,?)$
- $(9,16),\; (2,9),\; (9,2),\; (?,?)$
The quadrilaterals are all symmetrical. They may have rotational symmetry, or line symmetry, or both.
Can you work out what the missing coordinates are if you know they are all positive? Is there more than one way to find out?
Now plot those eight missing coordinates on a graph like the one below.
What shape do they make and what sort of symmetry does it have?
Why do this problem?
This problem is one that requires some familiarity with coordinates in the first quadrant. It will also call on knowledge of both rotational and line symmetry, and properties of various quadrilaterals.
Possible approach
You could play a game of 'twenty questions' to begin with so that pupils get a chance to familiarise themselves with properties of shapes. Choose a quadrilateral and write the name of it on a piece of paper. Invite the class to ask questions to guess what your quadrilateral is, but you can only answer yes or no. Keep a tally of the number of questions asked - if they get it in fewer than twenty, they win, otherwise you win. You could repeat this a few times with pupils choosing shapes.
Key questions
What kind of quadrilateral do you think this one is?
Where is its fourth vertex?
What kind of symmetry do you think this quadrilateral has? How do you know?
Possible support
Possible extension
Learners could plot their own quadrilaterals with one vertex of each forming a hexagon and so make a similar problem for a friend to try.