Can you traverse it?
How can you decide if a graph is traversable?
Problem
You might like to try The Bridges of Konigsberg before exploring this problem.
A traversable network is one you can draw without taking your pen off the paper, and without going over any edge twice.
For each network below, decide whether or not it is traversable. It might be helpful to keep a track of where you started, the route you took, and where you finished.
You may find it useful to download a printable copy of the networks
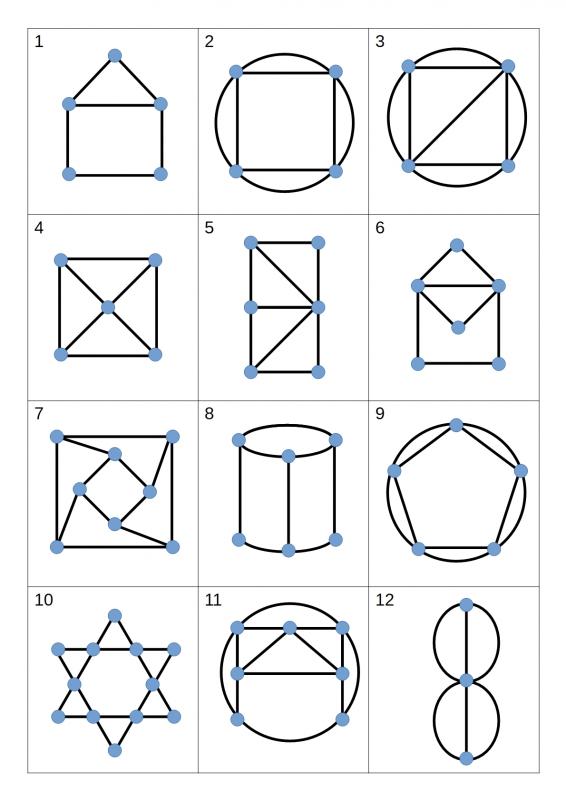
What do you notice about traversable networks where you started and finished in the same place?
What about traversable networks where you started and finished in different places?
What do you notice about the number of times you visited each vertex (point)?
For the networks which are not transversable, what is the smallest number of edges that you need to add (or remove) so that the resulting network is traversable?
Can you find a condition that guarantees a network is not traversable?
Can you explain why?
Getting Started
Why are the number of lines meeting at each vertex (point) important?
How can you be sure not to get stuck at a vertex?
Draw a traversable graph in which you can start and finish at the same vertex. What do you notice about the number of lines meeting at each vertex?
Student Solutions
Neel from Zurich International School in Switzerland and Miraya from Heckmondwike Grammar School in the UK found out which of the graphs are traversable. Miraya wrote:
My answers for whether or not each of the networks are [traversable]:
Q1) Yes
Q2) Yes
Q3) Yes
Q4) No
Q5) No
Q6) No (in fact graph 6 is traversable)
Q7) No
Q8) No
Q9) Yes
Q10) Yes
Q11) No (in fact graph 11 is traversable)
Q12) Yes
Nayanika from The Tiffin Girls' School in the UK thought about the start and end points of the traversable graphs:
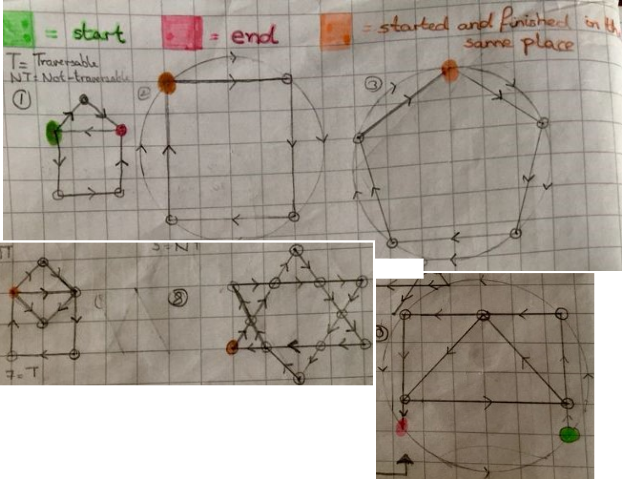
Miraya wrote:
For the traversable networks where I started and finished in the same place, I noticed that the shapes were generally the ones where simple shapes were put in circles because the method was to simply cover the inside shape then just go around the circle.
For the traversable networks where I started and finished in different places, I noticed that this was case for majority of the shapes. Being able to come up with shapes where you can cover all the sides but not start and finish in the same place is easier than ones where you have to start and finish in the same place.
The condition that I have come up with that guarantees whether a network is traversable or not is that if there is a centre vertex that you must cross multiple times in order to cover all the edges then it is very likely that the shape is not traversable.
Nayanika had a suggestion for choosing the starting point:
The nodes with the highest number(s) of routes to directly linked points are the potential beginning points.
Sajid from Wilson's School, James from Hamstel School, Hannah form Tring Park School for the Performing Arts and Roger from Westfield Academy, all in the UK, counted the number of routes connected to each point. This is James' diagram:

Hannah recorded these results in a table:
Adith from Mount Waverley Secondary College in Australia, Ilham from City of London School for Boys in the UK, M.Z. from Kings College Alicante in Spain, Lauren from TTS, Olivia from St Helen and St Katharine in England, Hannah, Sajid, James and Roger used these ideas to find a way of telling whether a network is traversable. Sajid wrote:
Originally, I came up with the hypothesis that 'if there is an odd number of nodes, the graph is not traversable'. However, upon further inspection, I found that some of the graphs that were traversable also had and odd number of nodes.
After a few thought-provoking minutes and a couple of false theories, I counted the number of edges connecting to each node. Finally, after all that work, I realised that the graphs that were traversable had a number of 0 or 2 odd nodes. Therefore, this meant that the untraversable graphs had a number other than 0 or 2 of odd nodes.
To explain why, James wrote:
I realised that there must be a route both into a point and out of it to make it traversable, this meant that if a graph had all even routes out of points then it would always be traversable. Also, if the routes are all even, then the route around the graph can start and finish at the same point, making it a complete circuit. (This means the starting/finishing point also has the same number of routes into it as out of it)
Lauren added:
If the network has only even vertices then it doesn't matter where you start.
(Even vertices = vertices with an even number of lines coming out of it)
Thinking about networks with two odd vertices, Adith wrote:
If you have exactly two vertices with an odd number of edges pointing towards it, then you will have to begin at one of the vertices and end at the other vertex.
Lauren added:
This is because if a vertex is odd, then it will have one line passing it on coming or on leaving, and one (or more) pair(s) of lines passing by it (on coming and on leaving).
Using and developing these ideas, Roger added and removed lines (edges) from the networks that were not traversable to make them traversable. Here is Roger's work. Click here to see a larger version. Click here to see Roger's full, detailed investigation.

Teachers' Resources
This problem offers a good opportunity to develop geometric reasoning, test ideas and formulate hypotheses and generalisations.
This problem featured in an NRICH Secondary webinar in September 2021.
