Can They Be Equal? Poster
Problem
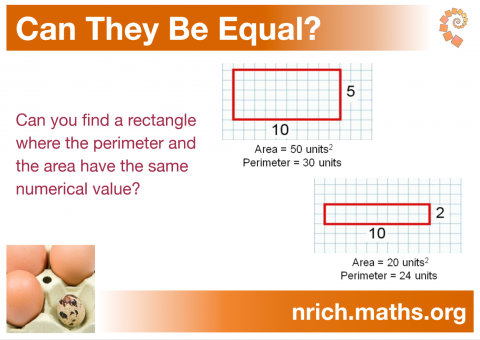
This poster is based on the problem Can They Be Equal?.
The poster is available as a PDF, or the image below can be clicked on to enlarge it.
Student Solutions
Using whole numbers only: 3 by 6 and 4 by 4
Using fractions: Any two numbers $a$ and $b$ where $a\gt2$ and $b = \frac{2a}{a-2}$
Why?
Geometrically

There are only two ways to make a rectangle using 4 squares.
These make 4 by 4 or 3 by 6 rectangles.
This extends to fractions if the sides of the red rectangle aren't whole numbers, but any two numbers which multiply to 4.
Algebraically
Sides $a$ and $b$
Perimeter: $2a+2b$
Area: $ab$
$2a+2b = ab$
Factorising to get whole number solutions:
$ab - 2a-2b = 0$
$(a-2)(b-2) = \underbrace{ab-2a-2b}_0+4 \therefore (a-2)(b-2)=4$
(This fits with the geometry above because the sides of the red rectangle are $a-2$ and $b-2$)
Whole number solutions: $a-2$ and $b-2$ are $1$ and $3$ or $2$ and $2$
$\therefore a$ and $b$ are $3$ and $6$ or $4$ and $4$
Other solutions: Find any two numbers which multiply to give $4$ and add $2$ to each of them
Rearranging to get infinitely many solutions
$\begin{align}ab-2b &= 2a\\
\Rightarrow b(a-2)&=2a\\
\Rightarrow b&=\frac{2a}{a-2}\end{align}$
$a$ and $b$ need to be positive $\therefore a\gt2.$ Infinitely many solutions.