Attractive rotations
Problem
Attractive Rotations printable sheet
Attractive Rotations printable sheet - extension
Take a look at the image below. How do you think it was created?
Did you notice any symmetry in the image?
Does this help you to imagine how the image was made?
Here is a diagram which shows how we created the image. We started with a triangle (shaded) and then used the coordinate grid to help us to rotate it through multiples of $90^{\circ}$ around the point $(0,0)$.
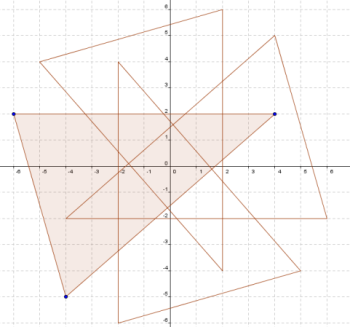
What do you notice about the rotational symmetry of your images?
What is the rotational symmetry of your final image if you rotate through multiples of $80^{\circ}$ or $135^{\circ}$? Can you explain why?
Send us pictures of your rotation patterns along with your interesting mathematical discoveries.
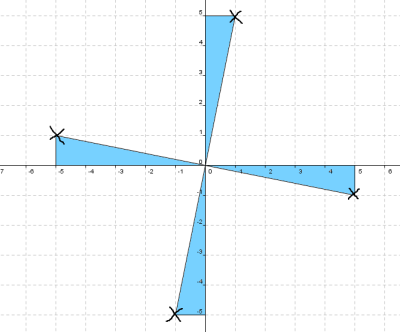
Getting Started
Student Solutions
Thank you to Sally and Emily from Parrs Wood for sending us pictures of their rotations. Here are their findings.
Sally noticed a pattern with the coordinates of our shape. 
In the table below, the coordinates (x',y') describe where the points (x,y) end up after they have rotated by $90^\circ$ around (0,0):
| (x,y) | (x',y') |
| (-4,-5) | (-5,4) |
| (-6,2) | (2,6) |
| (4,2) | (2,-4) |
| (-5,4) | (4,5) |
| (2,6) | (6,-2) |
| (2,-4) | (-4,-2) |
| (4,5) | (5,-4) |
| (6,-2) | (-2,6) |
| (-4,-2) | (-2,4) |
| (5,-4) | (-4,5) |
| (-2,6) | (2,-6) |
| (-2,4) | (4,2) |
So the coordinates (x',y'), which are a rotation of (x,y) by $90^{\circ}$ around (0,0), are (y, -x).
$180^{\circ}$ rotation is just two $90^{\circ}$ rotations so
(x,y) $\longrightarrow$ (x',y') = (y,-x) $\longrightarrow$ (y',-x') = (-x, -y).
$90^{\circ}$ $90^{\circ}$
I predicted rotations of $30^{\circ}$ would have rotational symmetry of order 12 and $72^{\circ}$ would have rotational symmetry of order 5 because $360\div30 = 12$ and $360\div72 = 5$. These were true for the pictures I drew. I also knew I couldn't colour in my $72^{\circ}$ rotation shape because 5 is prime so its only factors are 5 and 1.
$360\div80 = 4.5$ and I had to go round twice to complete my shape. This then gave me rotational symmetry of order 9 because $360\times2=720$ and $720\div80 = 9$.
As $360\div135 = 2{2\over3}$, I worked out $360\times3=1080$ and $1080\div135 = 8$ so I knew I had to go round 3 times to get a shape with rotational symmetry.
Mr Bakker sent us a photo of the work some of his students did on this task:
Do continue sending us pictures of your rotation patterns along with any interesting mathematical discoveries you make.
Teachers' Resources
Why do this problem?
This problem provides a simple starting point creating attractive patterns using rotations, with the potential to go much further - exploring rotational symmetry, understanding the relationship between coordinates when rotating through multiples of $90^{\circ}$, and practising accurate construction with ruler, compasses and protractor are just a few ideas.
Work on this problem could provide an excellent opportunity for forging cross-curricular links with Art and Design departments.
Possible approach
These printable resources may be useful: Attractive Rotations,
Attractive Rotations Extension.
Begin by showing learners this image, and give them the chance to discuss in pairs anything they notice about it. Share ideas, and ask learners to suggest how they think the image might have been created.
Key questions
How can you use a coordinate grid to help you to rotate each point through multiples of $90^{\circ}$ around $(0,0)$?
Can you use an isometric grid to rotate a shape through multiples of $60^{\circ}$?
What do you notice about the rotational symmetry of images based on rotations such as $30^{\circ}$ or $72^{\circ}$?
Possible support
Learners could begin by rotating single points through multiples of $90^{\circ}$ using the technique suggested below:
Possible extension
What is the rotational symmetry of your final image if you rotate through multiples of $80^{\circ}$ or $135^{\circ}$?