Angle of shot
Problem
When a projectile is fired, it travels along a parabola (in the absence of wind and air resistance).
Part 1: A shot putter will release the shot from arms length. Estimate the optimal angle that the shot should be released from to make it travel furthest, assuming the the shot putter can launch the shot at the same speed from any angle. (Note: the shot is launched from around head height rather than ground level)
Part 2: In reality it is not possible to launch the shot at the same speed from any angle: the body is naturally able to put more power into certain angles. Linthorne (2001) constructed a mathematical model in which the velocity is related to the projection angle as follows (Linthorne has written about the model on the Brunel University site; the published reference is given at the foot of the problem)
$$v= \sqrt{\frac{2(F-a\theta)l}{m}}$$
where $F$ is the force (in newtons) exerted on the shot for a horizontal release angle, $a$ is a constant that characterizes the rate of force decrease with increasing release angle, $l$ is the acceleration path length (in metres) of the shot during the delivery and $m$ is the mass of the shot $\left(7.26 \mathrm{kg}\right)$. A typical set of values for these parameters might be
$F=450\mathrm{N}$, $a=3\mathrm{N/degree}$, $l=1.65\mathrm{m}$ and $m=7.26\mathrm{kg}$.
Determine approximately the angle the shot putter should choose, to maximise the length of the shot put.
You may wish to do a little research and study some video footage or stills showing shot putters releasing the shot, to see how close your theoretical optimum angle is to the angle of release used in practice.
The published reference for the paper is Linthorne, N. P. (2001). Optimum release angle in the shot put. Journal of Sports Sciences, 19, 359-372.
Getting Started
Use a spreadsheet to work out different launch velocities, and hence range, for each angle.
Student Solutions
Assuming for the time being that the athlete can launch the shot at the same speed at any angle, I plotted a graph of range against projection angle for a variety of speeds:
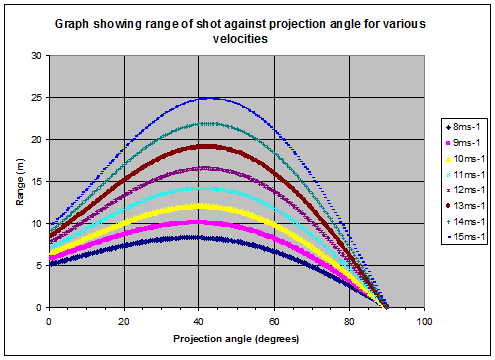
Looking at the graph, it appears the optimal angle for maximising range is slightly smaller than $45^{\circ}$.
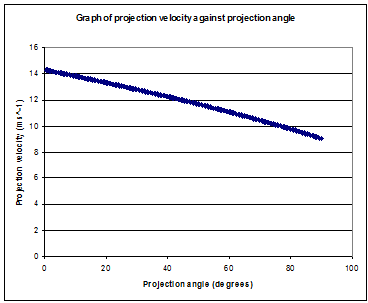
We now need to incorporate how the maximum launch speed varies with the projection angle. Here's a graph of projection velocity against projection angle. Although the projection velocity decreases as the projection angle increases, the range previously had a maximum at $45^{\circ}$, so the optimal angle will now be a tradeoff between angle and velocity.
We can now calculate the range of the shot using this projection velocity, and plot a graph of range against projection angle (using the same value of the parameters as before):
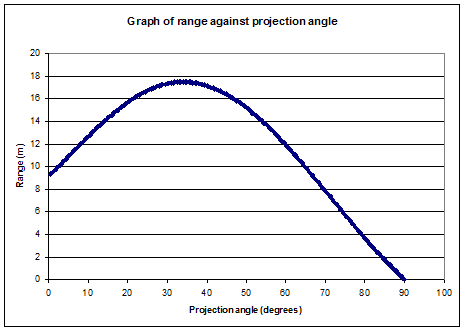
For these values of the parameters,we can see the optimal angle is now around $35^{\circ}$, as opposed to $45^{\circ}$ in the previous model.
Solving this problem using differentiation is quite messy, but well done to Joshua who had a go; you can see what he did here.
Teachers' Resources
Why do this problem?
This problem gives students the opportunity to investigate projectile motion in a real-life context.
Possible approach
Pose the first question, to work out the optimum angle of release for the shot, bearing in mind that the shot is released from above ground level - perhaps discuss and agree as a group what height to assume the release takes place.
Once students have tackled this first question, ask them to identify the different assumptions they have made. The key assumption is that equal force can be applied at all release angles. Invite students to speculate what variables affect the force (and hence velocity) with which the shot can be launched.
Introduce the equation for release velocity varying with angle, and then invite students to calculate the range for different launch angles. This is best done numerically, as a spreadsheet task.
Key questions
What are our modelling assumptions?
Are our assumptions valid?
Possible extension
Students may be interested in reading the article Modelling Assumptions in Mechanics.
Possible support
Cannon Balls could provide a good introduction to thinking about the mechanics of motion under gravity.