Angle Please
Weekly Problem 19 - 2017
In the figure, what is the value of x?
In the figure, what is the value of x?
Problem
Image
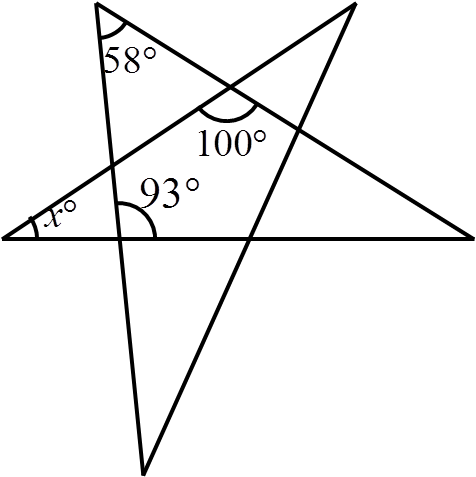
If you liked this problem, here is an NRICH task that challenges you to use similar mathematical ideas.
Student Solutions
There are two different ways of calculating the angle $x$.
Image
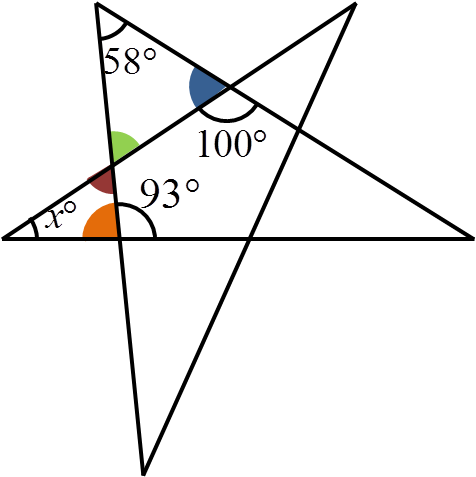
The blue angle can be calculated since angles on a straight line add to $180^\circ$. This means it is $180^\circ - 100^\circ = 80^\circ$.
The orange angle can be calculated similarly, to be $180^\circ - 93^\circ = 87^\circ$.
The green angle can then be calculated since the angles in the top-left triangle add up to $180^\circ$. This is $180^\circ - 80^\circ - 58^\circ = 42^\circ$.
The green and red angles are opposite angles. This means that they are equal, so the red angle is also $42^\circ$.
Then, the angles in the left-hand triangle must add up to $180^\circ$, so $x^\circ = 180^\circ - 42^\circ - 87^\circ= 51^\circ$.
Image
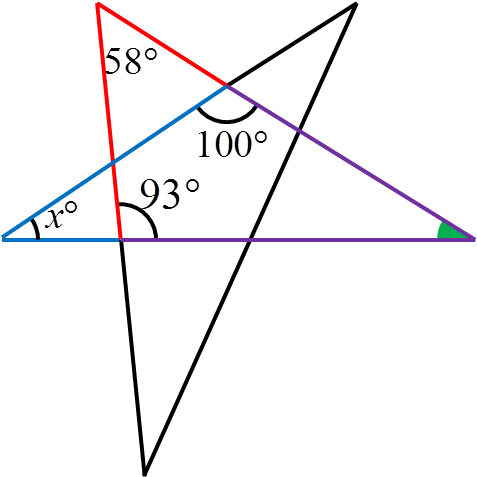
The angles in the red and purple triangle must add up to $180^\circ$, so the green angle is $180^\circ - 58^\circ - 93^\circ = 29^\circ$.
Then, the angles in the blue triangle must also add up to $180^\circ$. Therefore, $x^\circ = 180^\circ - 29^\circ - 100^\circ = 51^\circ$.
