Adding machine
Can you set the logic gates so that this machine can decide how many bulbs have been switched on?
Problem
In this problem a circuit has been set up to mimic a simple adding machine but the logic gates have all been set to AND by mistake.
By clicking on the blue squares you can change the type of logic gates.
There are three switches which you can turn on or off. There are two bulbs: one on the right and one on the left.
Can you find the combination of gate types such that:
- no bulb is on if no switch is on,
- the left-hand bulb is on and the right-hand bulb is off when exactly one switch is on
- the right-hand bulb is on and the left-hand bulb is off when exactly two switches are on
- and both bulbs are on if all three switches are on.
What do you think that this circuit represents?
Full Screen Version
You can read more about the mathematical aspects of logic and circuits in our article .
Getting Started
Work backwards or use a truth table.
Student Solutions
Two solvers cracked the circuit: Ruth from Manchester High School for Girls and Patrick from Woodbridge School. Rather nicely, they found different solutions to the problem. This raises the question: are there other solutions?
Ruth : I came up with the solution by considering the cases when each bulb lights. The right bulb lights when there are at least 2 switches on. This means that at least one pair of switches must be both on, so if you put each pair into an 'AND' gate to get a pair with both on then combine these with two 'OR' gates so that if any one of the 'AND' gates are lit, the bulb is lit, the bulb then lights when at least two are lit. The left bulb lights when either one or three switches are on. All three switches being on is quite easy: put the first two into an 'AND' gate and combine this with the third with another 'AND' gate. To get when exactly one is lit use two 'XOR' gates connected like the 'AND' gates. connect these two with an 'OR' gate into the left bulb.
Patrick correctly realised that this circuit is a 'binary adder' :
Patrick : The logic gates represent a simple counting device for binary - each switch counts for 1, the left light is the 1s column in binary, and the right light is the 2s column in binary. Thus, if no switch is on, the result is 0. If any one switch is on, the result is 1. If any two switches are on, the result is 2, which in binary is 10. If all three switches are on, the result is 3, which in binary is 11.
Ruth's and Patrick's solution circuits are :
Image
Image
Rather nicely, Ruth also noticed that a simpler circuit did the trick, and that some of the gates were redundant. This was an excellent piece of logical analysis!
"Another look at the circuit shows that we have 3 unecessary
gates: the 'AND' gates to give when 3 are on, and also the 'OR' to
combine this with the result of the 'XOR's, can be removed without
changing the output, as when all 3 are on the first 'XOR' is off,
so the second is on, as follows:
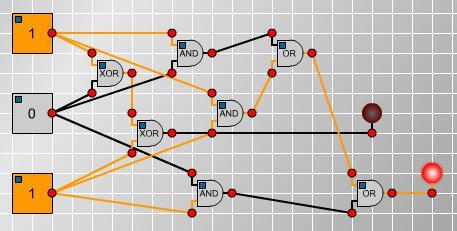
Image
Teachers' Resources
Why do this problem?
This problem is a complex exercise in logical manipulation. It will demand clear thinking on the part of the students.Possible approach
Some time will need to be spent in understanding the
description of the problem; students will need to be familiar with
the logic gates and their meanings.
Students might have difficulty understanding the conditional
statements 'If .... Then ....'
They should be encouraged to break down the statement into
small parts and interpret the language very precisely.
Key questions
The key to this problem is clear, systematic logical thinking
and breaking down the problem into manageable chunks
- What are the key features of the problem? What are we to change? What is fixed?
- What are the possible 'gates'?
- How many 'degrees of freedom' are there? How many constraints need to be met?
- In what way does this represent an 'adding machine'?
Possible extension
- Try the follow up question Circular Circuitry.
- Investigate other possible bulb outputs. Can the gates be chosen such that the bulbs are always on? always off?
- [hard] By linking together a sequence of these circuits, can students devise a way in which the total on 7 bulbs could be added up?
