Nicola's jigsaw
Problem

Nicola has a three dimensional puzzle made from cubes.
- There are six pieces altogether, but unfortunately one has gone missing
- All six pieces are different shapes
- The pieces fit together to make a 3 by 3 by 3 cube
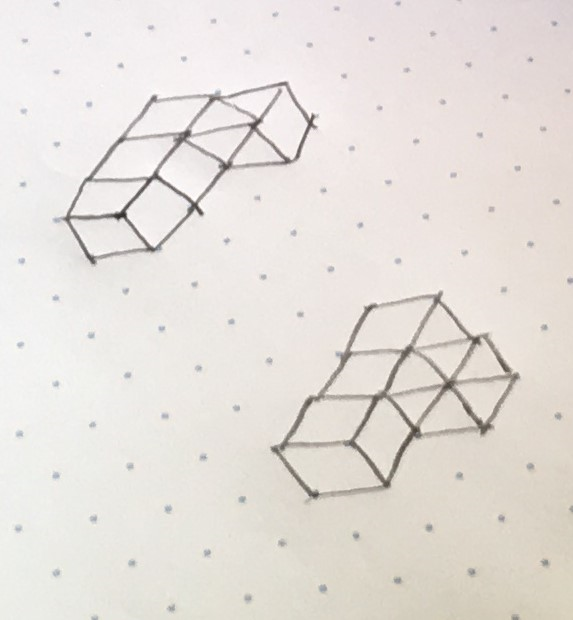
Here are diagrams showing five of the pieces:




Can you figure out what shape the sixth piece is?
Is there more than one possible shape that the sixth piece could be?
You may wish to use multilink cubes like the ones shown in the photo to help you solve the problem.
Many thanks to Nicola Coe who created the original task on which this problem is based.
Nicola has now produced this new version of the jigsaw. How many different arrangements of 4 blocks can you find to complete the 3x3x3 cube?
Getting Started
What is the volume of each piece?
What is the volume of the finished puzzle?
What is the volume of the missing piece?
What possible shapes could the missing piece be?
Student Solutions
This is Hope's method for finding the missing piece:
With the help of lego, I fiddled around with the puzzle pieces until I found a shape which almost finished the 3 x 3 area [volume] that the question asked for. So then I gathered extra lego blocks and softly placed them on the puzzle until I found the bricks that answered the solution.
Tim and Shahzaib from Greenacre Public School in Australia used a different method. Shahzaib wrote:
3 cubed equals to 27. That means the cube will be made of 27 blocks. If you add together the amount of blocks used in the picture, the answer will be 23. This means the sixth [piece] consists of 4 blocks.
So some people began by making different shapes from 4 small cubes.
Archie from Robert Hitcham primary school in the UK sent in a picture of two shapes which complete the puzzle:
Click here to see a picture of Archie with his shapes.
James from Newington College in Australia sent this photo of the cube built from the pieces available with one of Archie's shapes missing:

Khan Vy from BVIS Hanoi in Vietnam sent this video of building the cube using the other one of Archie's shapes.
Nabiha and Gianna from Greenacre Public School described these two shapes and also one more:
Throughout trial and error we discovered that there are possible constructions in a T format, a L format and a 2 by 2 piece.
Van Khanh and Byung Kwon from BVIS Hanoi sent this video showing them building the cube using the "2 by 2 piece".
Michelangelo from Bangkok Patana Schol in Thailand found another solution:
I used the Lego instruction method. Every time I add a piece it is light and the old one is dark. I also draw the piece I am adding. I think there must be more solutions but this is my one.
Kimlan from BVIS in Vietnam sent this video of completing the cube using the same piece.
Renea, Barney, Olivia, Zara, Sylvie and Eve and Millie, Mia, Imtiaz and Shafin from North Chadderton School in Manchester, UK, found these 5 pieces which could finish the cube:

The T shape, the L shape and the 2 by 2 block are included, but Michelangelo's cube is not - so that makes a total of 6 ways to finish the 3 by 3 cube.
Those are all of the possible ways, unless we use this idea described by Oliver and Luke from North Chadderon School to make more:
We have noticed that sometimes the missing [piece] is a rotation of previous pieces we found - if we add the rotations we have 8 variations of the missing piece.
Teachers' Resources
Why do this problem?
This problem offers students an opportunity to reason spatially in three dimensions, practise interpreting and drawing two dimensional representations of 3D shapes, and work systematically to find all the possible solutions to a problem.
Possible approach
The problem is much more manageable if students have cubes available to work with.
Introduce the problem and show students the diagrams of the five pieces:




Some students might want to start by making the five pictured pieces.
In order to find what the missing piece might look like, encourage students to consider what they know about volume to deduce how many cubes make up the missing piece.
They could then make each possible missing piece to see if it can be used to complete the puzzle, and use isometric paper to record their findings.
Nicola Coe has produced this revised version of her jigsaw puzzle, in which seven of the eight possible 4-block combinations can be used to complete the cube (the straight stick of 4 cubes can't fit in a 3x3x3 cube).
Key questions
What is the volume of each piece?
What is the volume of the finished puzzle?
What is the volume of the missing piece?
What possible shapes could the missing piece be?
Possible support
Students could work on The Third Dimension to practise working systematically and recording their work on isometric paper.
Possible extension
Nine Colours and Marbles in a Box offer suitable follow up challenges requiring reasoning in three dimensions.
