Fraction of a square
What fraction of this square is shaded?
Problem
Image
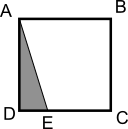
In the diagram, ABCD is a square.
The length CD is 4 times the length DE.
What fraction of the square is shaded?
This problem is taken from the World Mathematics Championships
Student Solutions
Drawing more little triangles
The length DE, which is the base of the triangle, fits 4 times along the side DC. So 4 copies of the triangle fit with their bases along DC:
Image
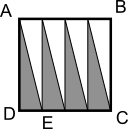
The white unshaded triangles are congruent to the grey shaded triangles, so they have the same area. There are 4 shaded triangles and 4 unshaded triangles, so there are 8 triangles altogether.
So the area of each triangle is $\frac18$ of the area of the square.
Finding the area of the square and the triangle
Suppose the square has side length $1$, so that its area is $1$. We can do this because we don't need to know what the area of the triangle is as a number, we just want to know it as a fraction of the area of the square. And finding numbers as fractions of $1$ is easy - for example, $\frac12$ of $1$ is just $\frac12$.
Then the height of the triangle is $1$, since it is the side length of the square.
$4\times=1$. So the length DE, which is the base of the triangle, is $\frac14$
So the area of the triangle is $\frac12\times\frac14\times1=\frac12\times\frac14=\frac18$
And $\frac18$ as a fraction of $1$ is just $\frac18$. So the area of the triangle is $\frac18$ of the area of the square.
