Graph Triangles
Use the information about the triangles on this graph to find the coordinates of the point where they touch.
Problem
This is the graph of the line $y=-2x+12$.
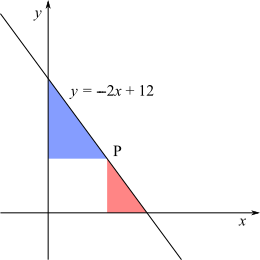
Point P is on this line.
The ratio of the area of the red triangle to the area of the blue triangle is $1:4$.
Find the coordinates of point $\text P$.
This problem is adapted from the World Mathematics Championships
Student Solutions
Answer: $(4,4)$
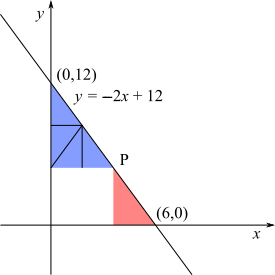
Using similar triangles
$y$-intercept: $x=0\Rightarrow y=12$
$x$-intercept: $y=0\Rightarrow 0=-2x+12\Rightarrow x=6$
Split the blue triangle into 4 congruent triangles, all similar to the blue triangle
$\therefore$ all congruent to the red triangle
$\therefore$ the base of the red triangle is $\frac13$ of $6$ and the height is $\frac13$ of $12$
$\Rightarrow\text{P}$ has coordinates $(4,4)$
Check:
$-2\times4+12=4$ so it is on the line $y=-2x+12$
Using length and area scale factors
$y$-intercept: $x=0\Rightarrow y=12$
$x$-intercept: $y=0\Rightarrow 0=-2x+12\Rightarrow x=6$
The area scale factor from the red to the blue triangle is $4$
$\therefore$ the length scale factor is $\sqrt4=2$
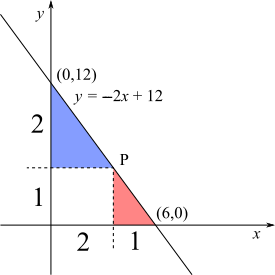
Base: total $6$ units
$6$ split in the ratio $2:1$ is $4:2$
$\Rightarrow x$ coordinate of $\text P$ is $4$.
Height: total $12$ units
$12$ split in the ratio $1:2$ is $4:8$
$\Rightarrow y$ coordinate of $\text P$ is $4$.
So $\text P$ is $(4,4)$.
Check:
$-2\times4+12=4$ so it is on the line $y=-2x+12$
Using the ratios between the sides of the triangles
$y$-intercept: $x=0\Rightarrow y=12$
$x$-intercept: $y=0\Rightarrow 0=-2x+12\Rightarrow x=6$

$y=-2x+12$ has gradient $-2$ so heights are twice bases
$\therefore a+b=6$ (adding the bases),
$2a+2b=12$ (adding the heights),
$2a=-2b+12$ ($\text P$ is on the line $y=-2x+12$), but those equations tell us the same information
Areas: $\frac12\times b\times2b=4\times\frac12\times a\times2a$
$\therefore b^2=4a^2\Rightarrow b^2=(2a)^2$, so $b=\pm2a$.
$a$ and $b$ are both positive, so $b=2a$.
$a+b=6$ gives $a+2a=6\Rightarrow3a=6$ so $a=2$.
So $b=2a=4$, and point $\text P $ is $(b,2a)=(4,4)$.
Using more algebra
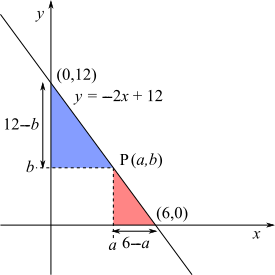
$y$-intercept: $x=0\Rightarrow y=12$
$x$-intercept: $y=0\Rightarrow 0=-2x+12\Rightarrow x=6$
$\text P$ lies on $y=-2x+12$ so $b=-2a+12$.
The area of the blue triangle is $4$ times the area of the red triangle, so:
Substitute $b=-2a+12$ into this:
$$\begin{align}&\tfrac12a\left(12-(-2a+12)\right)=4\times\tfrac12(6-a)(-2a+12)\\
\\
\Rightarrow & \tfrac12a(2a)=2\times(6-a)\left(2(6-a)\right)\\
\Rightarrow& a^2=\left(2\times(6-a)\right)^2\\
\Rightarrow& a=\pm2(6-a)\end{align}$$
$a$ and $6-a$ are both lengths on the graph so they are both positive so $a=2(6-a)$
$a=2(6-a)=\Rightarrow a=12-2a$ so $3a=12\Rightarrow a=4$
And $b=12-2a$, so $b=4$ too, and $\text P$ is $(4,4)$.
