A third of the area
The area of the small square is $\frac13$ of the area of the large square. What is $\frac xy$?
Problem
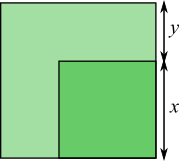
In this diagram, the area of the small square is $\dfrac13$ of the area of the large square.
Find $\dfrac xy$.
Image
This problem is taken from the World Mathematics Championships
Student Solutions
Answer: $\dfrac{1}{\sqrt3-1} = \dfrac{1+\sqrt3}2 =1.366$ to 3 d.p.
Using the relationship between the areas
The area of the small square is $\frac13$ of the area of the large square, so $$\frac {x^2}{(x+y)^2}=\frac13\Rightarrow\left(\frac x{x+y}\right)^2=\frac13\Rightarrow\frac x{x+y}=\dfrac1{\sqrt3}$$
We can make $\dfrac x y$ the subject of this equation:
$$\begin{align}\frac{x}{x+y}&=\frac1{\sqrt3}\\
\Rightarrow\sqrt3x&=x+y\\
\Rightarrow\sqrt3x-x&=y\\
\Rightarrow(\sqrt3-1)x&=y\\
\Rightarrow\frac x y &=\frac 1 {\sqrt3-1}\end{align}$$
To see how to express this as a fraction with a whole number denominator, see the bottom of the solution.
Splitting the larger square into smaller squares and rectangles
Image
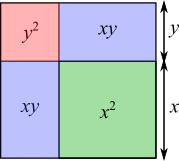
$\therefore$ red + blue = green $\times$ 2
$\Rightarrow y^2+2xy=2x^2$
$\Rightarrow 1+2\dfrac xy=2\dfrac{x^2}{y^2}$
Let $\dfrac xy=w$:
$$\begin{align}1+2w=2w^2&\Rightarrow 2w^2-2w-1=0\\
&\Rightarrow w^2-w-\tfrac12=0\\
&\Rightarrow\left(w-\tfrac12\right)^2-\tfrac14-\tfrac12=0\\
&\Rightarrow w-\tfrac12=\pm\tfrac{\sqrt3}{2}\\
&\Rightarrow w=\tfrac12\pm\tfrac{\sqrt3}{2}\text{ take the positive root since }w>0\\
&\Rightarrow w=\tfrac{1+\sqrt3}2\end{align}$$
Splitting the larger square into trapeziums
Image

Green square occupies a third of the area
$\therefore$ the three shapes have equal area
$\frac12\left(\left(x+y\right)+x\right)y=x^2$
Multiplying both sides of this equation by $2$ and expanding gives $2xy+y^2=2x^2$.
$\dfrac xy$ can be found from this equation as shown above.
