Grid Symmetry
How many ways can Mathias solve this symmetry challenge?
Problem
Mathias is given a grid of twelve small squares.
He is asked to shade exactly 4 of the squares so that the grid has 2 lines of reflection symmetry.
How many different grids could he produce?
This problem is taken from the UKMT Mathematical Challenges.
Student Solutions
The empty grid only has 2 lines of symmetry, as shown below, so when Mathias shades 4 squares, these will be the 2 lines of symmetry.

If Mathias shades one of the corner squares, then he must shade all of the corner squares, as shown below. That is one way to make a grid with 2 lines of symmetry by shading 4 squares.
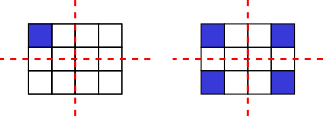
If Mathias shades one of the other squares on the top or bottom row, then he must also shade the square next to it and the two squares vertically opposite, as shown below. That is another way to make a grid with 2 lines of symmetry by shading 4 squares.
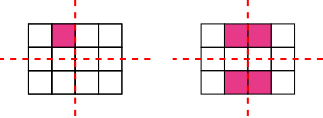
If Mathias shades a square along the middle row, then he must also shade the square opposite it on the middle row. But then only 2 squares will be shaded. The only other squares he can shade are the other two squares on the middle row, because he has to shade another 3 squares if he shades any of the squares along the top or bottom rows. This is shown below.
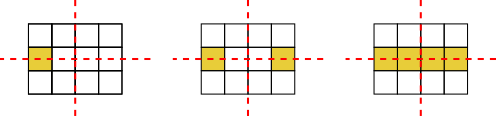
So shading the 4 squares along the middle row is the only other way to make a grid with 2 lines of symmetry by shading 4 squares.
So there are 3 ways to do it. This is shown more fully on this grid, which shows the yellow pattern, the blue pattern and the pink pattern.

As we have seen, if Mathias shades one of the blue squares, he must return the grid with the 4 blue squares. If he shades one of the pink squares, he must return the grid with the 4 pink squares. Or if shades one of the yellow squares, he must return the grid with the 4 yellow squares.
So he must return one of these 3 grids.
