Draining a pool
The water is being drained from a pool. After how long will the depth of the pool be 144 cm?
Problem
Image
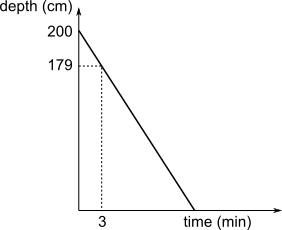
The graph shows the depth of the water, in centimetres, against time, in minutes.
At what time will the depth of the water be 144 cm?
Student Solutions
Answer: 8 minutes
Using similar triangles
Image

Image

Triangles are similar so 21 : 3 = 56 : ?
21 : 3 = 7 : 1
56 = 7$\times$8 so 56 : 8 is also the same as 7 : 1, ? = 8.
Using rates of change
In the first 3 minutes, the depth of the water decreases by 21 cm.
So in each 1 minute, depth decreases by 7 cm.
To reach 144 cm, it must decrease by 35 cm more, since 144 + 35 = 179.
35 = 7$\times$5, so it will take 5 more minutes, or 8 minutes in total.
Using gradients
Image

So the gradient of the line is $\frac{-21}3=-7$.
When the water level is $144$ cm, the depth of the water will have gone down by $56$ cm.
So, if this happens at time $t$, $\frac{-56}t=-7$, so $t=8$.
Using proportion
| time | decrease | final depth |
|---|---|---|
| 3 minutes | 21 cm | 179 cm |
| 3 more min | 21 cm | 158 cm |
| 1 more min | 7 cm | 151 cm |
| 1 more min | 7 cm | 144 cm |
Total 8 minutes.
Using congruent triangles
Because the graph is a straight line, we can use congruent triangles congruent to find other points on the graph, as shown on the right.
Image

Image

These three triangles have taken us too far, so we can now use smaller similar triangles to find more information:
Image

