Finding 3D stacks
Can you find a way of counting the spheres in these arrangements?
Problem
This activity may be used as a follow-on for those who have successfully worked at Doplication.
Let me help you visualise this representation of a 3D situation.
The picture below shows a 2 by 3 by 4 arrangement of red spheres, which you might see as two layers of 3 by 4:
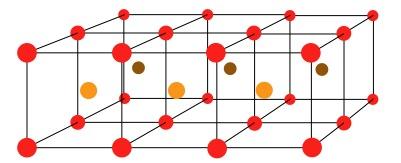
These two layers together could also be viewed as representing six cubes:
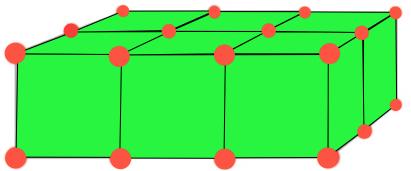
How many spheres are there altogether in this 2 by 3 by 4 arrangement?
How did you count them?
Use your system of counting to find the total number of spheres for other sizes, for example 3 by 3 by 3; 3 by 4 by 4; 4 by 4 by 5 etc.
How would you find the number of spheres for any sized arrangement?
Getting Started
To start with you may find it helpful to use some materials (e.g. straws and Blutak) to create a model of the arrangement of red spheres.
Student Solutions
We haven't received many solutions to this task yet. Bertie from Dame Bradbury's School in England sent in this formula:
C = (L - 1) x (W - 1) x (D - 1)
I wonder what Bertie means by this? If you have any ideas about this, or if you'd like to share some different ideas about this task with us, then please email us.
Teachers' Resources
Why do this problem?
Possible approach
You could show the group the images in the problem and invite them to 'say what they see'. Facilitate discussion amongst learners so that the structure of the arrangement is clear.
Ask learners to work on the questions in pairs and then bring them together at a suitable point to check that everyone agrees with the total number of spheres. Encourage them to articulate how they are going about counting and record the different ways on the board for all to see. (Pairs may then stick with their own approach or adopt someone else's.)
Once they have had the opportunity to count several examples (a spreadsheet might be useful for recording these), challenge pupils to move from the particular to the general. Give them time to compose instructions for counting the spheres for any size grid. Once language-based instructions have been created, help them move to a formula. Depending on the children's experience, you could do this as a whole group by choosing one method and working on it together.
Key questions
Possible extension
Learners could compare the 3 by 3 by 3 arrangement of this challenge with the 3 by 3 of Doplication; then the 4 by 4 and 5 by 5 and so on.
Possible support
The visualisation may be difficult for some so using construction materials may be helpful.
