Square and triangle

Image

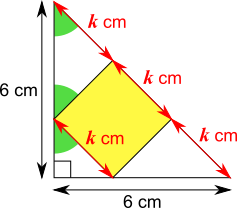
The sides of the large right-angled triangle are both 6 cm, so its angles are 90$^\circ$, 45$^\circ$, and 45$^\circ$.

The angles in the square are all right angles, so the smaller triangles around the square are also right-angled isosceles triangles. 

This means that the angles shaded green on the diagram are all 45$^\circ$, and the lengths labelled $k$ cm are all equal to the side length of the square.

This is important for all of the three methods shown below:

Using congruent triangles

Image

 Since the lines in the diagram are all horizontal, vertical or at $45^\circ$, it can be split up using horizontal and vertical lines as shown. Now all of the triangles are congruent to the smallest triangle, at the bottom left corner of the original diagram.

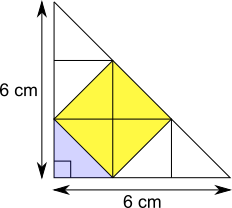
There are 9 of these triangles altogether, and 4 of them fit into the square, so the area of the square is $\frac49$ of the area of the whole triangle.

The area of the whole triangle is $\frac12\times6\times6 = 18$ cm$^2$. So the area of the square is $\frac49$ of $18$ cm$^2$, which is $8$ cm$^2$.

Using scale factors

The diagonal side of the whole triangle is equal to 3$k$ cm, and the diagonal side of the small triangle in its corner (to the bottom left of the square) is $k$ cm. So the scale factor from the small triangle to the whole triangle is 3.

Image

 

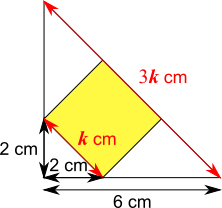
This means that the sides of the small triangle are 2 cm, since 2 cm $\times$ 3 = 6 cm.

So the area of the small triangle is 2$\times$2$\div$2 = 2 cm$^2$.

The area of the whole triangle is 6$\times$6$\div$2 = 18 cm$^2$.

So the area of the square and the two triangles on either side of it is 18 $-$ 2 = 16 cm$^2$. Each of these two triangles is congruent to half of the square, so the square occupies half of this area. So the area of the square is 8 cm$^2$.

Using Pythagoras' Theorem on the whole triangle

Image

 

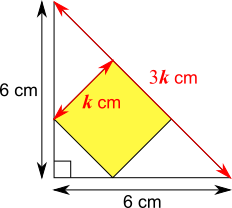
The hypotenuse of the triangle is equal to $3k$, and can also be found using Pythagoras' Theorem: $$6^2+6^2=(3k)^2\\\Rightarrow 72=9k^2\\

\Rightarrow 8=k^2$$ But $k^2$ is the area of the square. So the area of the square is $8$ cm$^2$.